Représentations du groupe symétrique d'indice trois - Définition

Introduction

En mathématiques les représentations du groupe symétrique d'indice trois noté S₃ sont un exemple simple d'application de la théorie des représentations d'un groupe fini.

Sur un corps de caractéristique nulle et contenant toutes les racines sixièmes de l'unité, il existe trois représentations irréductibles du groupe symétrique d'indice trois, la représentation triviale, celle correspondant à la signature et une d'ordre deux correspondant aux isométries linéaires laissant invariant un triangle équilatéral.

L'analyse des représentations de S₃ est une illustration des concepts comme le théorème de Maschke, le caractère, la représentation régulière, les représentations induites et la réciprocité de Frobenius. Les constructions des différentes représentations sont ici réalisées manuellement, ce que permet la petitesse de l'ordre du groupe.

Représentations du groupe S3

Représentation régulière

Le groupe est d'ordre suffisamment limité pour permettre une représentation matricielle exhaustive de la représentation régulière. Si cette méthode est trop lourde pour être envisagé ne serait-ce que pour S₄, elle est ici praticable.

Le groupe S₃ contient six éléments et trois classes de conjugaison, la première ne contient que l'identité noté 1, la deuxième les transpositions t₁ = (23), t₂ = (13) et t₃ = (12) et la troisième les deux cycles d'ordre trois c₁ = (123) et c₂ = (132). Si V est l'espace vectoriel de la représentation régulière, alors (1, c₁, c₂, t₁, t₂, t₃) est la base canonique de la représentation, à l'ordre près.

Soit ρ le morphisme de groupe de S₃ dans le groupe général linéaire GL(V) de V. Soit x et y deux éléments de G et donc de la base de V. Par définition de la représentation régulière, ρ_x(y) = xy. On en déduit les matrices M_x de la représentation :

On remarque l'existence de deux vecteurs propres pour toutes les images de ρ :

Toute permutation laisse f₁ invariant, toute permutation paire laisse f₂ invariant et toute permutation impaire transforme f₂ en -f₂. On obtient ainsi deux représentations de degré un, l'une t est la représentation triviale, associant un à chaque élément de S₃, l'autre σ associe la signature. Ces représentations sont de degré un donc irréductibles.

Théorème de Maschke

Recherchons les autres représentations, le théorème de Maschke indique qu'elles sont toutes sommes directes de représentations irréductibles, il suffit donc de connaître toutes les représentations irréductibles.

Tout sous-espace vectoriel stable pour la représentation possède un supplémentaire stable pour cette représentation, le théorème de Maschke indique une méthode pour le trouver. Soit F l'espace vectoriel engendré par f₁ et f₂ et p le projecteur sur F parallèlement à l'espace engendré par c₁, c₂, t₁, t₂, alors le projecteur p₀ défini par l'égalité suivante possède un noyau stable par toutes les images de ρ.

Dans la base canonique, on obtient les matrices P et P₀ des deux projecteurs :

Notons G le noyau de p₀. Le projecteur p₀ est composé de deux matrices bloc égales, c'est la matrice du projecteur dont le noyau est composé des vecteurs colonnes de somme nulle. Notons G le noyau de p₀. Si j désigne la racine cubique de l'unité, alors on obtient la base suivante de G

Considérons alors la représentation (G, φ) la représentation où φ est la restriction de ρ à G. Si G_x est la matrice de φ_x dans la base (g_i) pour x élément de S₃, on obtient :

Représentation de S₃ comme groupe des isométries du triangle

On remarque alors que l'espace vectoriel H engendré par g₁ et g₃ est un sous-espace stable par φ, il possède le supplémentaire engendré par g₂ et g₄ aussi stable et dont la représentation est isomorphe à celle de H. Soit θ la restriction de φ à H, (H, θ) est une représentation de degré deux, elle est présente deux fois dans la représentation ρ. Cette représentation est irréductible car sinon ρ serait une représentation de matrices diagonales et son ensemble d'arrivé serait un groupe abélien, ce qui est impossible car ce groupe est isomorphe à S₃ qui ne l'est pas.

Considérons la base de H composée des deux vecteurs suivants h₁ = g₁ + g₃ et h₁ = i.(g₁ - g₃) où i désigne un complexe imaginaire de carré égal à -1. Soit H_x la matrice de θ_x dans cette base. On a alors :

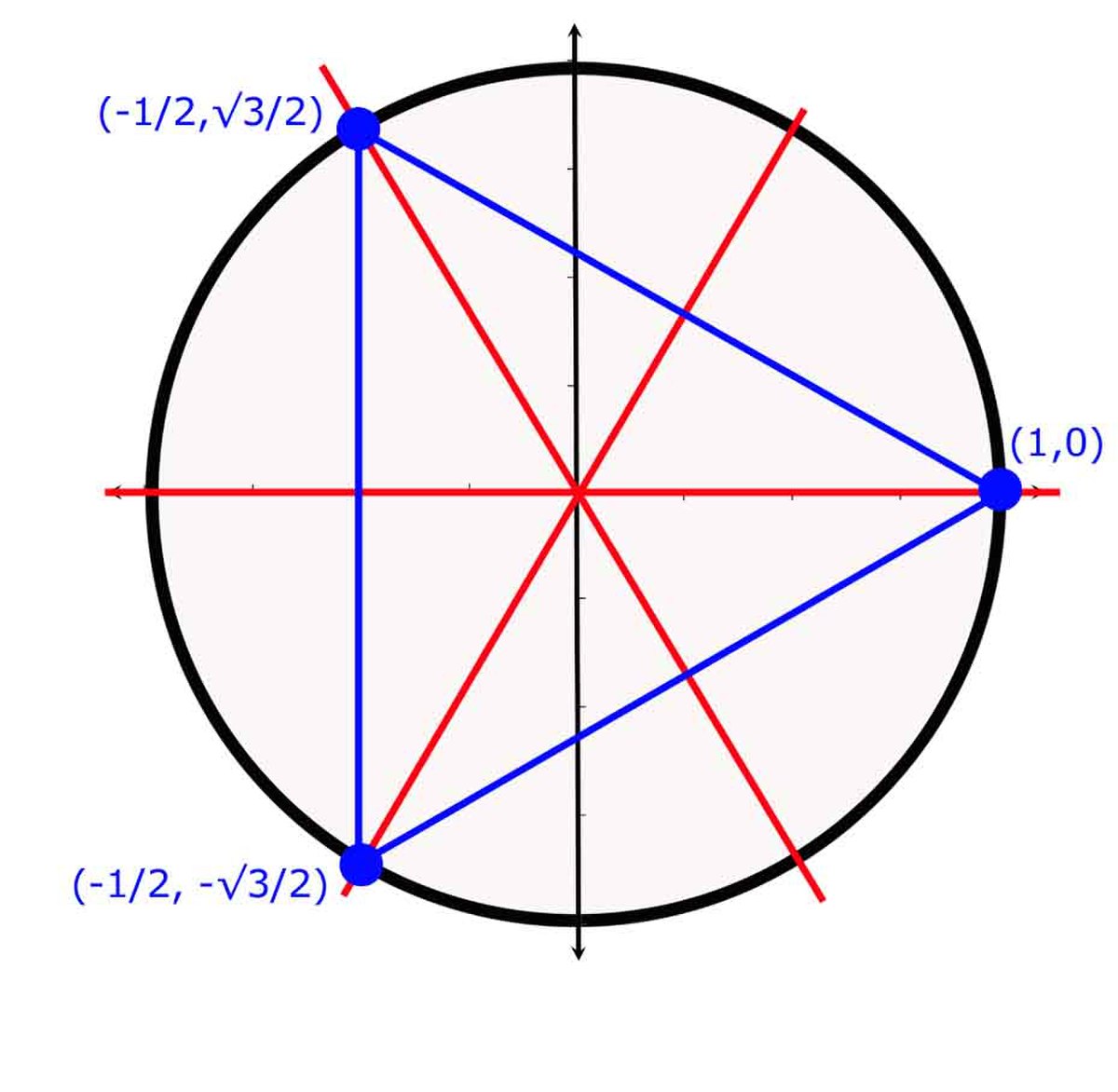
On reconnaît le groupe diédral du triangle représenté sur la figure de droite, les rotations c₁ et c₂ sont au nombre de deux, elle déplace le point 1 vers j ou j₂ si le plan est identifié au plan complexe, les trois symétries, correspondant aux transpositions ont un axe représenté en rouge sur la figure.

En conclusion, la représentation régulière est composée d'une somme directe de quatre représentations : deux de degré un, la représentation triviale et celle associée à la signature, et deux de degré deux, isomorphes et correspondant aux applications linéaires laissant un triangle invariant.