Revêtement (mathématiques) - Définition

Exemples

Revêtement du cercle par une droite

Soit S¹ le cercle dans le plan . La droite réelle est alors un revêtement de S¹ défini par l'application :

.

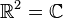
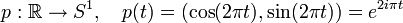
Chaque fibre est ici infinie dénombrable ( ).

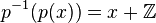
La construction se généralise au revêtement exponentiel du tore :

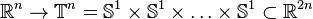
La fibre est dénombrable : ( ).

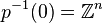
Les fonctions puissances

L'application du plan complexe privé de l'origine

définit un revêtement.

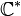
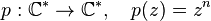
Chaque fibre est ici finie et a n élements.

L'application exponentielle

L'application du plan complexe

définit un revêtement.

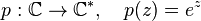
Chaque fibre est ici infinie dénombrable ( ).

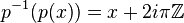
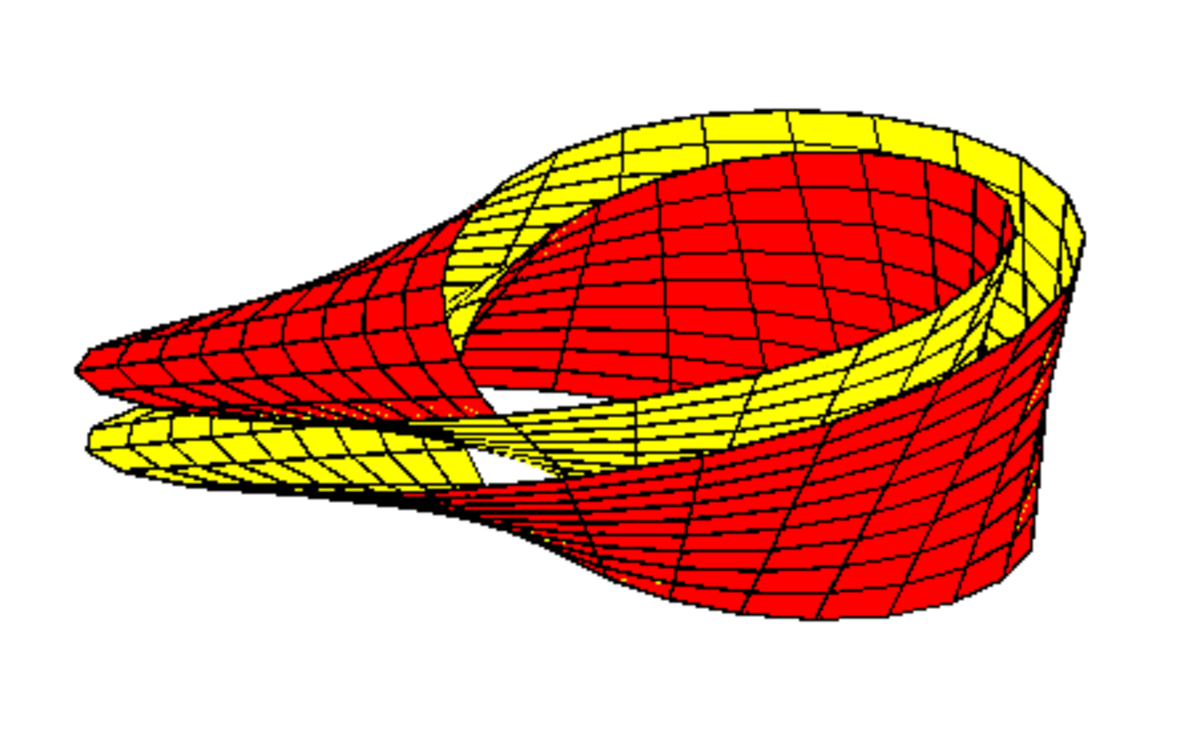
La bande de Möbius

Le cylindre (ou anneau) est un revêtement à deux feuillets de la bande de Möbius.

La bande de Möbius est une variété topologique non orientable alors que son revêtement est orientable. On montre plus généralement que tout variété connexe non orientable possède un revêtement connexe à deux feuillets orientable. C'est le cas notamment du plan projectif dont le revêtement est une sphère (voir ci-dessous), et de la bouteille de Klein dont le revêtement est le tore.

Revêtement de l'espace projectif

Pour n>1, l'application canonique est un revêtement de l'espace projectif (réel) ; la fibre a deux éléments.

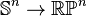
Dans le cas du plan projectif dont une représentation dans est donnée par la surface de Boy, il est possible de transformer la sphère par immersion en un revêtement à deux feuillets de cette surface de Boy. Si on fait se traverser ces deux feuillets, on procède alors à un retournement de la sphère.

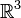
On procède de même pour le retournement du tore, après avoir fait coïncider celui-ci en un revêtement à deux feuillets de la bouteille de Klein.

Revêtements universels

Un revêtement universel d'un espace B est un revêtement galoisien E tel que tout revêtement soit isomorphe à un revêtement associé à E (non nécessairement connexe). C’est-à-dire que pour tout revêtement D de B, il existe un morphisme de E sur D.

Deux revêtements universels sont isomorphes et tout revêtement d'un revêtement universel est trivial.

Théorème — Un revêtement simplement connexe E est un revêtement universel.

Théorème — Un espace (connexe par arcs) B admet un revêtement simplement connexe si et seulement s'il est semi-localement simplement connexe.

En particulier tout graphe, toute variété topologique admet un revêtement simplement connexe.

Théorie des revêtements

Morphismes et transformations de revêtements

Un morphisme de revêtements au-dessus de B est une application continue qui commute avec les projections π_X et π_X', c'est-à-dire telle que . Les applications identiques Id_X sont des morphismes. La composée de deux morphismes est un morphisme. Donc les revêtements de base B avec leurs morphismes forment une catégorie .

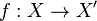
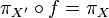
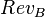
Revêtements sur un segment

Théorème — Tout revêtement sur un intervalle compact [a;b] de R est trivial.

C'est un cas particulier du théorème plus général :

Théorème — Tout espace fibré, localement trivial, sur un intervalle compact [a;b] de R est trivial.

Relèvement des chemins

Proposition — Soit (X,π) un revêtement de B, b un point de B, soit . Soit c un chemin d'origine b Alors il existe un chemin et un seul dans X d'origine x tel que .

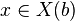
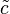
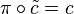
Monodromie des lacets et relèvement des applications

Le groupe fondamental de la base, , opère par une action de groupe à droite sur la fibre .

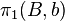
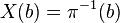
Revêtements galoisiens et groupe de Galois d'un revêtement

Un revêtement est dit galoisien (ou régulier ou normal) s'il est connexe par arcs et le groupe des automorphismes agit transitivement sur la fibre de chaque point.