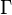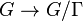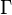Revêtement (mathématiques) - Définition

Introduction

Revêtement du cercle X par une hélice Y, les ensembles disjoints S_i sont projetés homéomorphiquement sur U.

En mathématiques, et plus particulièrement en topologie et en topologie algébrique, un revêtement d'un espace topologique B par un espace topologique E est une application continue et surjective p : E → B telle que tout point admette un voisinage ouvert U tel que l'image réciproque de U par p soit une union disjointe d'ouverts de E, chacun homéomorphe à U par p.

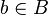
Il s'agit d'un cas particulier de fibré, localement trivial, à fibre discrète. Les revêtements jouent un rôle pour calculer le groupe fondamental et les groupes d'homotopie d'un espace. Un résultat de la théorie des revêtements est que si B est connexe par arcs et localement simplement connexe, il y a une correspondance bijective entre les revêtements connexes par arcs de B, à isomorphisme près, et les sous-groupes du groupe fondamental de B.

Définition mathématique et terminologie

Homéomorphismes locaux au-dessus de B

Un homéomorphisme local est une application continue appelée projection telle que si x est un point de X, il existe un voisinage ouvert U de x et un voisinage ouvert V de π(x) tels que la restriction de π à l'ouvert U soit un homéomorphisme sur V. Si B est un espace topologique, un espace X muni d'un homéomorphisme local est appelé espace étalé au-dessus de B.

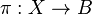
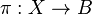
B est appelé la base. Pour tout point , on appelle fibre de X au-dessus du point b et on note X(b) le sous espace . On appelle section (continue) de X au-dessus de B, une application continue telle que .

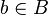
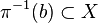
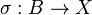
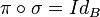
Par exemple, une submersion entre variétés différentielles de même dimension est un homéomorphisme local.

Revêtements

Un revêtement d'un espace topologique B est un espace X, muni d'un homéomorphisme local surjectif, tel que si b est un point de B, il existe un voisinage V de b, un espace discret F (non vide) et un homéomorphisme qui commute avec les projections sur l'espace B, c'est-à-dire que si , π(Φ ^{− 1}(b,f)) = b.

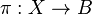
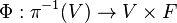
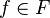
La définition précédente est celle d'un fibré, localement trivial, à fibre discrète avec la remarque que si la base B n'est pas connexe, la fibre F dépend du point base b et s'identifie à la fibre π ^{− 1}(b).

Chaque application est une section de π ^{− 1}(V) au-dessus de l'ouvert V. Autrement dit est la réunion disjointe des ouverts tous homéomorphes par π à V.

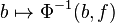
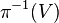
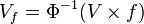
Théorème : Soit p un homéomorphisme local dont toutes les fibres sont finies de même cardinal n (non nul), alors p est un revêtement fini.

Revêtements triviaux

Si F est un espace discret, l'application définit un revêtement au-dessus de B. Plus généralement, un revêtement est dit trivial si on peut prendre V=B dans la définition, c'est-à-dire s'il existe un espace discret F et un homéomorphisme qui commute avec les projections sur l'espace B, c'est-à-dire que si , π(Φ ^{− 1}(b,f)) = b. Un homéomorphisme est un exemple de revêtement trivial.

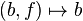
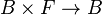
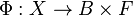
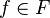
Constructions de revêtements

Produit fibré, Somme directe, Changement de base

Soit X, Y et Z trois espaces topologiques, un morphisme (application continue) de X dans Z et ψ de Y dans Z. On appelle produit fibré de X et Y par rapport à Z, noté , un espace topologique, , un morphisme, p_X, de ce produit dans X et p_Y de ce produit dans Y tels que pour tout espace topologique, A et deux morphismes, f (de A dans X) et g (de A dans Y) tels que , alors il existe un morphisme, p_A de A dans le produit, tel que et .

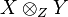
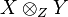
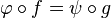
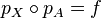
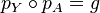
Groupes discrets opérant proprement et librement

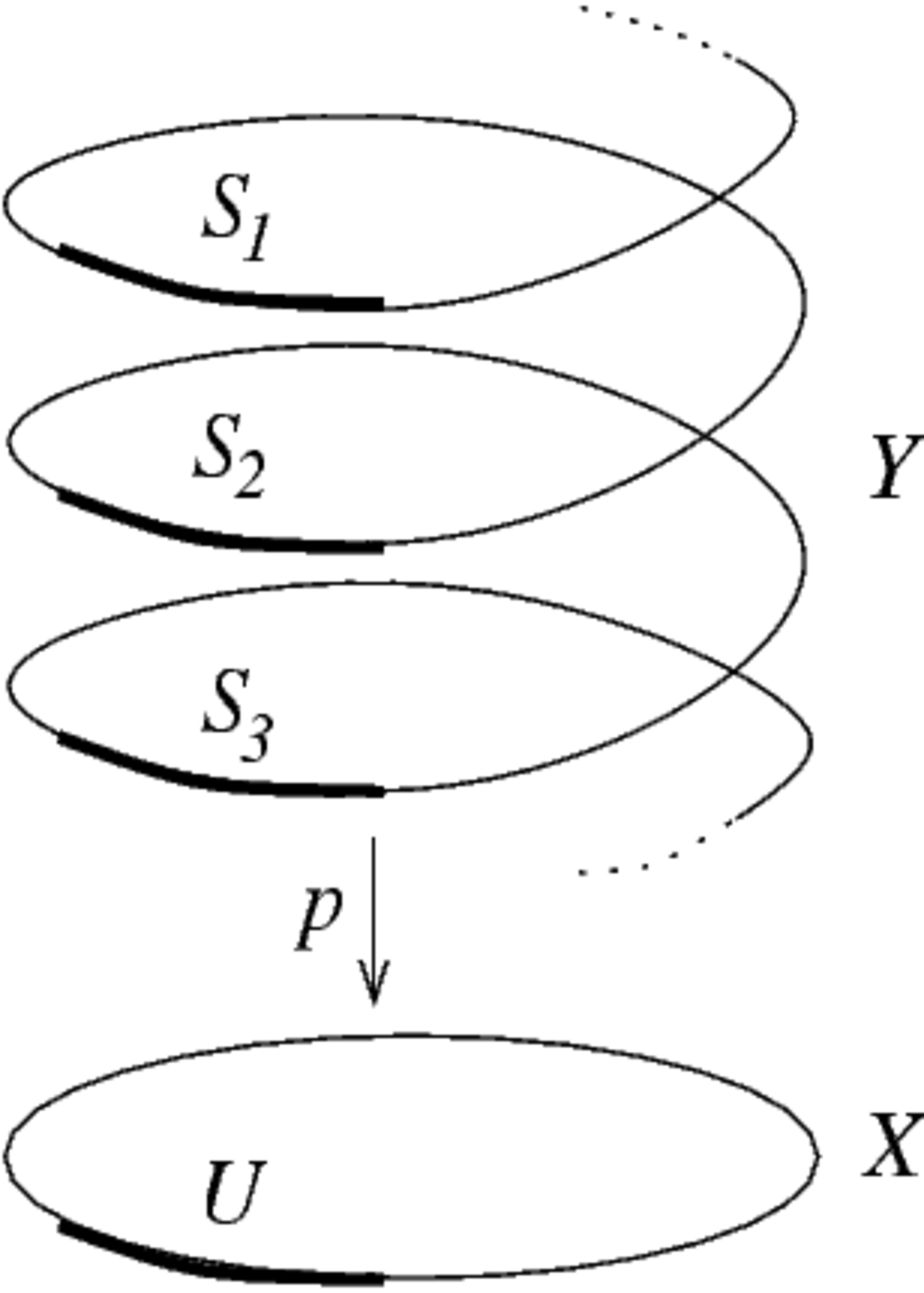
Soit G un groupe discret opérant proprement et librement sur un espace localement compact E, la projection définit un revêtement de fibre G.

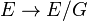
En particulier, si est un sous-groupe discret du groupe topologique G, la projection est un revêtement de fibre .

Construction de revêtements par recollement