Signe (arithmétique) - Définition

Signe d'une fonction

Une fonction à valeurs réelles est dite positive si sa valeur est positive en chaque point de son domaine de définition. Elle est dite négative si sa valeur est négative en chaque point de son domaine de définition. Une fonction positive et négative (à la fois) a donc toutes ses valeurs positives et négatives à la fois, donc est constante de valeur nulle.

Pour décrire le signe d'une fonction qui admet certaines valeurs strictement positives et d'autres strictement négatives, il est nécessaire de préciser les domaines relatifs à chaque signe. Dans le cas d'une fonction continue sur une réunion d'intervalles réels, ces domaines sont eux-mêmes des intervalles dont il suffit de préciser les bornes.

Fonction affine

Le signe d'une fonction affine est complètement déterminé par le signe de son coefficient directeur et de la valeur de son éventuel point d'annulation.

• Si le coefficient directeur est strictement positif, la fonction est négative sur l'intervalle à gauche du point d'annulation et positive sur l'intervalle à droite de ce point.
• Si le coefficient directeur est strictement négatif, la fonction est positive sur l'intervalle à gauche du point d'annulation et négative sur l'intervalle à droite de ce point.
• Si le coefficient directeur est nul, la fonction est constante et son signe également.

Tableau de signe

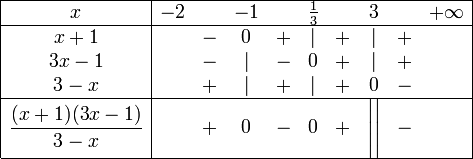
Étant donné une expression algébrique factorisée (c'est-à-dire un produit ou un quotient) dans laquelle le signe de chaque facteur est connu, dépendant d'une seule variable réelle, le tableau de signe de cette expression comprend une ligne pour la variable, une ligne pour chaque facteur et une ligne pour l'expression complète. La première ligne (celle de la variable) comprend toutes les valeurs d'annulation des différents facteurs et les bornes du domaine d'étude. Des traits verticaux sous ces valeurs déterminent les colonnes du tableau.

Chaque ligne de facteur est munie de zéros sur les traits verticaux correspondant aux valeurs d'annulation du facteur considéré. Dans chaque colonne est indiqué le signe de chaque facteur sur l'intervalle de valeurs considéré.

Les signes sur la ligne du résultat sont définis par la règle des signes à partir des signes présents dans la colonne. Chaque trait vertical dans cette ligne est muni de zéro lorsqu'il y en a un en facteur multiplicatif (c'est-à-dire au numérateur). Une double barre marque un trait vertical lorsqu'un zéro survient au dénominateur.

Fonction du second degré

Le signe d'une fonction du second degré ne dépend que du signe de son coefficient dominant et de la valeur de ses racines, ces dernières pouvant être déterminées à l'aide du discriminant.

• Si le discriminant est strictement négatif, la fonction est de signe constant (celui de son coefficient dominant) et ne s'annule pas.
• Si le discriminant est nul, la fonction est de signe constant (celui de son coefficient dominant) et ne s'annule qu'en un point.
• Si le discriminant est strictement positif, la fonction est du signe de son coefficient dominant en dehors des racines ; elle est du signe opposé entre les racines.

Règles opératoires

Les opérations d'addition et de multiplication ont été étendues aux nombres négatifs de façon à préserver les propriétés d'associativité, de commutativité et de distributivité. D'autres propriétés valables pour les nombres positifs doivent cependant être reformulées, par exemple :

• deux nombres positifs rangés dans l'ordre ont leurs carrés rangés dans le même ordre ;
• deux nombres de même signe rangés dans l'ordre ont leur inverse rangés dans l'ordre contraire.

Addition et soustraction

Une somme algébrique est une suite d'addition et de soustraction de nombres positifs ou négatifs, employant éventuellement des parenthèses. Elle peut être réinterprétée avec les règles suivantes :

• la soustraction d'un nombre négatif est l'addition de sa valeur absolue ;
• l'addition d'un nombre négatif est la soustraction de sa valeur absolue.

Règle des signes

La règle des signes permet de déterminer le signe de leur produit à partir des signes de chaque facteur.

Cette règle peut être étendue à un nombre quelconque de facteurs :