Nombre négatif - Définition

Introduction

Un nombre négatif est un nombre réel qui est inférieur (inférieur ou égal) à zéro, tel que −3 ou −π.

Généralités

les nombres négatifs comprennent les entiers négatifs, les nombres rationnels négatifs, les nombres irrationnels négatifs, les nombres réels négatifs. Zéro compte comme un nombre négatif.

Lorsqu'un nombre est négatif et non nul, il est dit strictement négatif. Lorsque nous parlons de nombres positifs ou négatifs, les adjectifs positif et négatif doivent être pris au sens large, c'est-à-dire que zéro est inclus ; zéro est donc un nombre (le seul) à la fois positif et négatif. Si nous considérons des nombres positifs ou négatifs mais non nuls, alors nous devons préciser strictement positifs ou strictement négatifs.

Les entiers négatifs peuvent être regardés comme une extension des entiers naturels, telle que l'équation x − y = z ait une solution significative pour toutes les valeurs de x et y ; l'ensemble des entiers positifs et négatifs s'appelle l'ensemble des entiers relatifs. Les autres ensembles de nombres peuvent être alors construits, comme des extensions progressivement plus élaborées ou comme des généralisations à partir des entiers.

• L'ensemble des entiers relatifs négatifs est habituellement noté ,
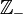
• l'ensemble des entiers relatifs strictement négatifs est habituellement noté ,
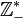
• l'ensemble des nombres rationnels négatifs est habituellement noté ,
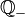
• l'ensemble des nombres rationnels strictement négatifs est habituellement noté ,
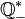
• l'ensemble des nombres réels négatifs est habituellement noté ,
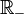
• l'ensemble des nombres réels strictement négatifs est habituellement noté ,

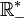
En comptabilité on les représentent par des nombres écrits en rouge, ou par un nombre entre parenthèses.

Interprétation

Les nombres négatifs ont du sens pour :

• représenter des dettes ou des déficits (par opposition à des patrimoines positifs)
• représenter des pertes ou plus généralement des variations "en moins". Exemple : des descentes (d'échelle ou d'ascenseur), par opposition à des montées représentées par des chiffres positifs ; des destructions (annulations, suppressions, etc.) par opposition à des créations (accroissements etc.) représentées par des nombres positifs ; ...
• décrire des valeurs sur une échelle qui descend au-dessous d'une référence préalablement fixée (un zéro), telle que la température, le repérage de niveaux de sous-sol, la profondeur d'immersion sous le niveau de la mer...
• compter une quantité manquante, par rapport à une référence. Exemples : un vide dans un objet plein ; des manquants dans une unité militaire par rapport à son effectif nominal ; la graduation d'une balance sans le plateau qui sert à contenir les objets à peser (elle est a zéro avec le plateau, donc en dessous quand on l'enlève)...

Histoire

La première apparition connue des nombres négatifs est dans Les Neuf Chapitres sur l'art mathématique (Jiu zhang suan-shu), dont les versions qui nous sont parvenues datent du début de la dynastie Han (IIe siècle av. J.-C), sans qu'on puisse dater les versions originales, sans soute plus anciennes. Les Neufs Chapitres utilise des bâtons de numération rouges pour les nombres positifs et des noirs pour les negatifs.. Cela permettait aux chinois de résoudre un système d'équations linéaires à coefficients négatifs.

En Inde on formule des règles cohérentes pour les travailler, et on comprend leur signification (en même temps que celui du zéro) dans des situations telle que les emprunts et dettes, ainsi qu'en atteste les ouvrages de Brahmagupta (VII^e siècle), bien que ces concepts peuvent être antérieurs. Brahmagupta utilise les nombres négatifs dans l'équation du second degré et sa solution ; son vocabulaire est celui du commerce (un nombre négatif est une dette, un nombre positif une richesse).

Les concepts indiens se diffusent lentement vers l'ouest ; vers l'an 1000 les mathématiciens arabo-musulmans utilisent couramment le zéro et les nombres négatifs (pour représenter des dettes, encore), et l'occident entre en contact avec ces concepts.

Cependant la notion de quantité négative reste longtemps choquante ; lorsque des nombres négatifs apparaissent on les considère comme "absurdes" ou faux. Par exemple Diophante (III^e siècle), à propos de l'équation 4x + 20 = 0, dont la solution est -5, dit qu'elle est absurde. En Inde, Bhaskara (XII^e siècle) utilise les nombres négatifs mais rejette les solutions négatives de l'équation quadratique, il les considère comme inadéquates et impossible à interpréter ; on fera de même en occident au moins jusqu'au (XVIII^e siècle). On s'autorise néanmoins à s'en servir, quitte à les appeler absurdes comme Nicolas Chuquet (XV^e siècle) qui s'en sert comme exposant.

Les mathématiciens occidentaux résistent au concept, sauf dans le contexte commercial (toujours) où on peut les interpréter comme des dettes (Fibonacci, chapitre 13 de Liber Abaci, 1202) ou des pertes (Fibonacci, Floss, 1225).

Les nombre négatifs acquièrent progressivement droit de cité au cours du (XIX^e siècle), pour n'être véritablement acceptés qu'avec le (XX^e siècle)