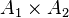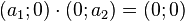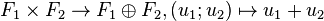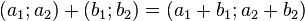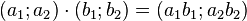Somme directe - Définition

Propriété universelle de la somme directe

Soit A un anneau ; soit une famille de A-modules, N un A-module ; soit une famille d'applications linéaires.

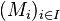
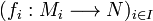
Alors il existe une unique application A-linéaire telle que : , avec l'injection canonique.

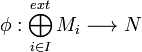
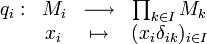
Par analyse synthèse :

• Supposons qu'un tel φ existe. Soit  ; on a :

avec δ_ik symbole de Kronecker ; on a : et, pour , φ((x_n + x_m) = φ((x_n,0) + (0,x_m)) = f_n(x_n) + f_m(x_m) par A-linéarité, donc ce qui assure l'unicité de φ

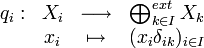
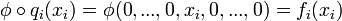
• Posons donc  ; les f_i étant linéaires, φ est linéaire.

Soit , on a :  ; ainsi nous avons bien , donc φ existe bien.

 

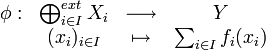
Somme directe externe et produit cartésien

Lorsque deux sous-espaces F₁, F₂ d'un espace vectoriel E sont en somme directe, l'application suivante est bijective :

Il existe dans ce cas une unique structure d'espace vectoriel sur le produit cartésien telle que cette application soit un isomorphisme d'espaces vectoriels ; la loi interne et la loi externe sont définies respectivement par les relations :

et ,

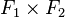
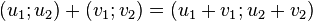
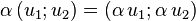
où u₁, v₁ sont dans F₁, u₂, v₂ sont dans F₂, et α est dans K.

Ceci incite, si E₁ et E₂ sont deux espaces vectoriels quelconques sur le même corps K, à définir leur somme directe, dite alors externe.

Somme directe externe de deux K-espaces vectoriels

La somme directe externe de deux K-espaces vectoriels E₁ et E₂ est le produit cartésien sur lequel on définit

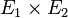
• une addition :

• une multiplication externe par les éléments de K :

(où )

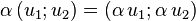
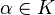
Muni de ces deux lois de composition, l'ensemble est un espace vectoriel sur K.

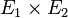
Dès lors, et sont deux sous-espaces de , respectivement isomorphes à E₁ et E₂ (on a "plongé" E₁, E₂ dans le produit cartésien) ; la relation justifie l'appellation de somme directe externe.

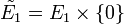
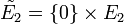
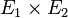
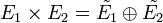
Lorsque E₁ et E₂ sont de dimensions finies, il en est de même de leur somme directe externe, et :

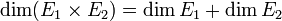
(car est somme directe des deux sous-espaces et , qui ont même dimension que , respectivement).

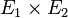
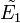
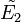
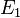
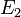
Somme directe externe de plusieurs K-espaces vectoriels

On définit de même la somme directe externe de k espaces vectoriels sur le même corps K.

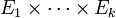
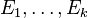
Lorsque sont de dimensions finies, il en est de même de leur somme directe externe, et :

.

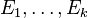
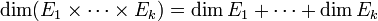
Somme directe externe d'une famille infinie de K-espaces vectoriels

Pour un nombre fini d'espace vectoriels la somme directe externe et le produit direct coïncident. Il n'en est pas de même lorsque la famille est infinie.

En effet, soit une famille (éventuellement infinie) de K-espaces vectoriels. La somme directe externe est le sous-espace vectoriel du produit direct constitué des familles à support fini. La propriété universelle ci-dessous est la raison de ce choix.

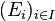
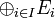
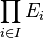
On peut, avec cette notion, élégamment définir la somme directe d'une famille infinie de sous-espaces : Une famille de sous-espace de E est en somme directe si et seulement si le morphisme somme qui va de la somme directe externe de ces sous-espaces dans E qui à une famille de vecteurs associe leur somme est injectif.

Remarque à propos d'autres structures algébriques

On définit de manière analogue la somme directe externe d'un nombre fini de groupes additifs, ou d'anneaux, ou de A-modules sur le même anneau A.

Par exemple, si A₁ et A₂ sont deux anneaux, on définit sur deux lois de composition interne :

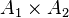
• une addition :

• une multiplication :

Muni de ces deux lois de composition, l'ensemble est un anneau. Même si A₁ et A₂ sont intègres, leur produit cartésien ne l'est pas : a₁, a₂ étant deux éléments non nuls de A₁, A₂ respectivement, on a : .