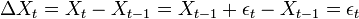Stationnarité d'une série temporelle - Définition
La liste des auteurs de cet article est disponible ici.
Types de non-stationnarité
Lorsqu'une ou plus des conditions de stationnarité n'est pas remplie, la série est dite non-stationnaire. Ce terme recouvre cependant de nombreux types de non-stationnarité, dont deux sont ici exposés.
Stationnarité en tendance
Définition — Une série est stationnaire en tendance si la série obtenue en "enlevant" la tendance temporelle de la série originale est stationnaire.
La tendance temporelle (ou trend en anglais) d'une série chronologique est sa composante liée au temps.
Exemple: Soit le processus suivant:
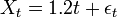
Ce processus est non-stationnaire car son espérance augmente avec le temps (condition 1 violée). Mais la série Yt obtenue en soustrayant l'effet de la tendance temporelle, Yt = Xt − 1.2t est stationnaire:
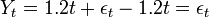
Stationnarité en différence
Définition — Une série est stationnaire en différence si la série obtenue en différenciant les valeurs de la série originale est stationnaire.
L'opérateur de différence est noté: ΔXt = Xt − Xt − 1
Ordre d'intégration d'une série temporelle
Définition — Une série temporelle est dite intégrée d'ordre d, que l'on note I(d), si la série obtenue après d différenciations est stationnaire.
Exemple: Soit la marche aléatoire pure:
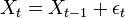
On peut montrer qu'une marche aléatoire n'est pas stationnaire. On voit ici qu'elle est intégrée d'ordre 1, la série des différences est en effet stationnaire: