Synchronisation dans les repères tournants - Définition

La synchronisation sur le disque immobile

Regardons maintenant le problème de la synchronisation sur le disque d'un peu plus près.

Nous avons une procédure pour synchroniser les horloges d'un même repère. Mais cette procédure nous l'avons exploitée dans le cas des repères inertiels.

Connaissant la relativité restreinte et connaissant cette procédure, comment l'appliquer dans le repère en rotation R' ?

La simultanéité est déterminée par le temps indiqué par les horloges. Simultané est synonyme de "temps identique indiqué par deux horloges".

Par conséquent la procédure de synchronisation revient à s'assurer que deux horloges immobiles dans un repère indiquant le même temps correspondent à des événements simultanés.

La notion de repère en relativité sera bien définie si on peut parsemer le repère d'horloges synchronisées, c’est-à-dire si on sait rendre tous les points du repère simultanés (surface de simultanéité ou lieu où tous les points sont simultanés). Si ce n'était pas le cas, on aurait alors un sérieux problème pour attribuer une coordonnée temporelle à certains événements dans ce repère.

Prenons 4 événements et 4 observateurs immobiles dans un repère R inertiel donné.

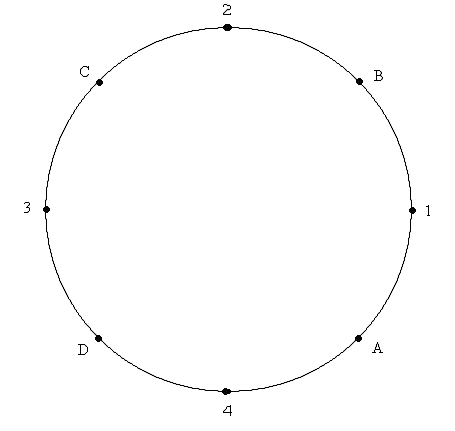
On a 4 observateurs 1, 2, 3 et 4, tous immobiles dans le repère inertiel R. Et 4 événements A, B, C et D ayant lieu aux endroits indiqués.

Attention, ce n'est pas parce que nous avons dessiné un cercle qu'il y a rotation. Cela indique seulement la disposition des événements et observateurs.

Les événements sont choisis de manière à pouvoir effectuer les synchronisations. A et B sont simultanés pour 1. B et C simultanés pour 2. C et D simultanés pour 3. Et D et A simultanés pour 4.

1 et 2 étant immobiles dans le repère inertiel. Alors, A et B seront également simultanés pour 2. Et donc C et A. De même, C et B et A et B seront simultanés pour 3, et donc D et A. Enfin, pour 4, A, B, C et D sont bien tous simultanés. Tout est cohérent.

C'est même assez trivial puisque le repère inertiel est spatialement euclidien en relativité restreinte par hypothèse. Les distances sont donc parfaitement définies et l'immobilité relative garantie. Et donc aussi les simultanéités.

Nous avons déjà signalé qu'un espace-temps plat, et donc un espace plat et la géométrie euclidienne, garantit que la procédure de synchronisation habituelle est consistante.

Mais même si cela semble trivial, nous utiliserons cette procédure de manière nettement plus délicate plus loin.

Soit une classe de repères accélérés (avec tous la même accélération par rapport à R). Avec une accélération constante et uniforme. Alors, ce que nous venons de voir reste valable. En effet, soit 1 et 2 deux observateurs définissant deux repères R' et R" accélérés et initialement au repos (par exemple, ou en tout cas avec la même vitesse à l'instant initial). Alors, l'accélération uniforme garantit que la vitesse de 1 et 2 restera identique à tout instant dans R et la distance entre 1 et 2 constante dans R. Par conséquent, 1 et 2 sont immobiles l'un par rapport à l'autre et on peut appliquer la procédure précédente pour synchroniser toutes les horloges dans, par exemple, R'.

D'un point de vue dynamique, dans cette classe de repères accélérés, on doit ajouter une force virtuelle. Mais d'un point de vue cinématique, tout reste valable au sein de cette classe de repères accélérés.

Signalons toutefois que les accélérations peuvent être vicieuses. Et il y a un défaut avec le raisonnement ci-dessus. Pouvez-vous voir lequel ?

Si les accélérations sont identiques dans R, alors dans R' la distance qui joint 1 et 2 doit augmenter (par simple application de la contraction des longueurs). Par conséquent ils ne sont pas immobiles l'un par rapport à l'autre dans R' ! Pour garantir que les observateurs sont immobiles dans R' il faut que 1 et 2 aient des accélérations légèrement différentes dans R. Ce n'est pas très difficile à calculer et à réaliser (il faut que la distance qui les sépare dans R diminue exactement de la même manière que la contraction des longueurs). Alors R' aura un ensemble d'observateurs immobiles qui peuvent effectuer une synchronisation.

On voit qu'il y a déjà des difficultés avec de simples accélérations linéaires (nous n'approfondirons pas cela ici, mais l'espace n'y est déjà plus euclidien et le repère est appelé repère de Rindler, voir les références).

Rien n'interdit, a priori, d'étudier le mouvement d'un objet accéléré, même en rotation. Mais rien ne garantit que les formules de Lorentz gardent leur forme dans un repère en rotation car l'accélération n'est pas uniforme dans tout le repère. De même, la synchronisation devient non triviale comme nous allons le voir.