Synchronisation dans les repères tournants - Définition

Différentes synchronisations

Il existe une infinité de manière de synchroniser les horloges. En fait, il est possible d'effectuer des transformations quelconques des coordonnées sans changer la physique.

C'est juste une transformation mathématique, elle ne doit pas avoir de conséquence sur les phénomènes physiques. C'est une simple reparamétrisation des coordonnées. Si ce sont les coordonnées d'un repère "physique" donné (c’est-à-dire un repère attaché à un objet physique), les transformations sont dites internes au repère. On dit aussi que c'est une transformation de jauge.

Un observable physique est une quantité qui dépend du repère considéré mais sa description doit être indépendante de la reparamétrisation choisie. C’est-à-dire que la quantité doit être invariante de jauge. Cattaneo a développé de telles techniques et vous trouverez plus amples informations sur sa méthode dans les références.

Ici, nous allons seulement nous intéresser à la synchronisation des horloges.

La question qui se pose ici est "quelle est la synchronisation la plus adaptée à la description de l'effet Sagnac ?"

Un changement quelconque du système de coordonnées est donné par les fonctions arbitraires :

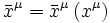
Avec la condition supplémentaire pour ne pas changer la flèche du temps et donc assurer la causalité.

Les transformations sont encore trop générales. Nous allons ici seulement nous intéresser à une transformation introduite par Selleri.

On choisit un repère de référence, par exemple le repère inertiel R, et on modifie les coordonnées dans R1 en fonction de la vitesse par rapport à R.

Si on se limite à la synchronisation des horloges, on se limite alors aux transformations

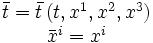
où les coordonnées sont celles obtenues avec la synchronisation d'Einstein habituelle que nous avons vue. Et les coordonnées surlignées sont celles du nouveau système de coordonnées.

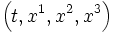
Attention, il ne s'agit pas ici d'un changement de repère et de transformations dans le style des transformations de Lorentz. Ici il s'agit de deux systèmes de coordonnées attachés au même repère.

La transformation de Selleri est donnée par :

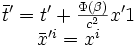
On choisit arbitrairement un repère absolu (par exemple le repère inertiel R dans l'effet Sagnac) dans lequel les coordonnées sont identiques aux coordonnées obtenues par la synchronisation d'Einstein. Et dans un autre repère R1 en mouvement dans une direction donnée x¹ avec la vitesse β = V / c, on utilise les relations ci-dessus où Φ est une fonction arbitraire. Attention et t' (respectivement et x'ⁱ) ne sont, à nouveau, pas les coordonnées dans les repères R et R1 mais uniquement les coordonnées dans R1 selon deux méthodes de synchronisation, tandis que β fait bien référence à R !

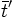
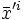
On peut écrire cette fonction comme

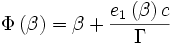
e₁ est appelé le paramètre de Selleri. Lorsque e₁ = − βΓ / c, on retrouve la synchronisation habituelle et lorsque e₁ = 0, on trouve la synchronisation de Selleri ou jauge de Selleri. Cette synchronisation est dite "absolue" car elle utilise un repère absolu comme base pour la synchronisation de tous les repères.

Dans la jauge de Selleri, le changement de coordonnées vaut simplement

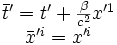
Dans la jauge de Selleri, les transformations de Lorentz du temps prennent une forme particulièrement simple :

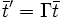
(où ici et se réfèrent aux repères R et R1, dans la jauge de Selleri).

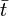
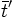
Dans cette jauge la transformation du temps d'un repère à l'autre est particulièrement simple et liée à la dilatation du temps et pas à la position, ce qui justifie mieux son appellation de synchronisation absolue (elle ne dépend pas de la position des repères).

Dans la jauge de Selleri la simultanéité est absolue mais, étant donné que l'on utilise une synchronisation différente (et donc des heures différentes indiquées par les horloges), il ne s'agit pas de la même simultanéité que celle affirmée relative avec la synchronisation d'Einstein.

Par contre, dans la jauge de Selleri, la vitesse de la lumière est réellement anisotrope dans R1.

En fait, la jauge de Selleri a l'avantage de définir un découpage de l'espace-temps en surfaces spatiales qui est indépendant du repère considéré.

Mais cela n'a rien de magique. Ce découpage en surface spatiale est juste celui obtenu avec la synchronisation habituelle dans le repère R. Et comme celui-ci est considéré comme absolu dans la jauge de Selleri, dire que ce feuilletage est indépendant du repère revient en fait à dire qu'on choisit le feuilletage de R et qu'on le considère comme la référence unique.

Selleri, comme la majorité des auteurs, est d'accord pour dire que le choix de la jauge est juste une convention. Mais il affirme que dans le cas de la rotation c'est différent, sa jauge étant indispensable.

Qu'en est-il en réalité ? Récapitulons les avantages et inconvénients des jauges de Selleri et d'Einstein.

• Physiquement, l'emploi de l'une ou l'autre jauge est équivalent. La physique doit être indépendante de la jauge et on peut toujours passer des résultats numériques d'une jauge à une autre jauge par l'emploi de la transformation, purement mathématique, adéquate.
• Si l'on souhaite disposer d'une synchronisation globale pour le disque, il faut utiliser la jauge de Selleri qui consiste en fait à utiliser la synchronisation d'Einstein dans le repère R.
• Si l'on souhaite une description complète des relations entre les vitesses locales, les temps propres, etc. Il est plus facile d'utiliser la jauge d'Einstein.
• La synchronisation d'Einstein est basée, comme nous l'avons vu sur des signaux lumineux (locaux si l'on synchronise de proche en proche). Elle garantit ainsi une isotropie optique : elle correspond à ce qu'on "voit" compte tenu de vitesse de propagation des signaux. C'est la synchronisation "naturelle".

L'effet Sagnac est universel : le décalage temporel ne dépend pas de la vitesse des signaux utilisés.

• L'anisotropie locale des signaux est artificielle dans Selleri (paramètre de Selleri), en particulier pour des signaux de vitesse inférieure à c. Elle est fonction de la vitesse de rotation et l'anisotropie n'est donc pas liée à la géométrie (au rayon du disque). Sa seule interprétation physique est qu'elle est proportionnelle à la force centripète (centrifuge dans R'). Or celle-ci est perpendiculaire à l'anisotropie et ne peut justifier son sens. L'anisotropie est donc arbitraire car on ne peut pas lui trouver de relation avec quelques choses de physique et local. On voit mal comment la vitesse locale d'un signal peut être influencée par le fait que d'autres signaux peuvent effectuer un parcourt global (le tour du disque) particulier (comme dans le paradoxe de Selleri).
• Dans la jauge d'Einstein, il n'est pas besoin d'introduire une anisotropie locale arbitraire. L'anisotropie globale ayant une signification géométrique claire. Et la seule condition, dans tous les cas (effet universel), est l'isotropie dans tout repère local.
• Rappelons que le principe de relativité est une condition naturelle, un idéal, que l'on doit respecter. Or la jauge de Selleri viole explicitement ce principe. Même si l'on considère des repères R1, R2,... inertiels, la synchronisation de Selleri viole le principe de relativité. Cela n'a rien d'étonnant puisque l'on choisit arbitrairement un repère absolu ce qui n'est qu'une décision de nature mathématique et non physique. Puisque cette violation existe aussi dans des repères inertiels, cela montre aussi que ce choix ne peut être lié à l'existence d'un effet physique tel que la force centrifuge.

Il est toujours possible, en violant le principe de relativité, de choisir un repère absolu arbitraire et de décréter que ce sont ses horloges qui dictent le temps et pas les horloges en mouvement. Il suffit en tout point de tout repère de lire le temps sur l'horloge de R située à cet endroit au moment où on la voit passer (c'est encore plus radical que la synchronisation de Selleri et illustre bien le caractère artificiel). Mais le temps ainsi défini dans R1 est totalement abstrait. Il ne correspond pas à la synchronisation naturelle (la vitesse des signaux, par exemple, dépendrait de leur sens, totalement arbitrairement, sans raison apparente, alors que leur durée aller-retour serait identique) et pire le temps ainsi défini ne correspond pas à ce qu'un observateur de R1 noterait sur une horloge qu'il transporte avec lui.

Le choix de Selleri est un peu plus subtil que ça (il tient compte de la dilatation du temps) mais reste totalement arbitraire.

Tandis que dans la jauge d'Einstein, le principe de relativité est respecté. Par contre on a bien la présence d'un repère R privilégié dû à l'existence de la rotation. Celle-ci a des effets physiques qui justifient une modification de la géométrie et une violation globale du principe de relativité (lorsque les signaux font un tour du disque, ce qui est manifestement relié à la rotation). Tandis que localement (isotropie de la vitesse de la lumière) le principe est respecté. Il y a quelque chose de physique qui doit être responsable de cette rotation (sinon O' continuerait tout droit), des forces centripètes, dirigées vers le centre du cercle, qui le maintiennent en rotation. Quelle que soit la nature de ces forces, il existe quelque chose de physique, lié à R, qui est responsable de la rotation est justifie que dans R' la situation est différente. Et cette fois, contrairement à la jauge de Selleri, en passant aux repères inertiels, la violation disparaît en même temps que la cause physique.

Il semble donc que la synchronisation d'Einstein soit la plus appropriée à la fois pour décrire les aspects physiques mais aussi en toute généralité (pas seulement pour Sagnac), sans devoir artificiellement choisir un repère absolu, en adoptant la même procédure dans tout repère inertiel local. C’est-à-dire que la jauge d'Einstein est covariante.

Mais rappelons que cela reste un choix (comme choisir la jauge de Coulomb, non covariante, en électromagnétisme), une convention, et la seule chose importante lorsque l'on affirme un certain nombre de chose en relativité est de toujours bien préciser la synchronisation utilisée et le fait que les résultats inhabituels présentés ne sont éventuellement qu'un artefact dû au choix de la jauge. C’est-à-dire qu'il faut présenter les résultats physiques en s'affranchissant de la synchronisation. Par exemple, ce que voit (au sens propre) un observateur (par exemple le rythme apparent d'une horloge distante, comme dans l'effet Doppler) ou ce qu'il mesure localement (par exemple les instants de tels événements ou le temps mis par un signal pour faire le tour du disque) ne doit pas dépendre de la synchronisation.

Vous pouvez vérifier quelle est la vitesse des signaux dans R1 dans la jauge de Selleri. Vous verrez qu'il est possible pour certains signaux de remonter le temps ! Alors qu'ils ne le font pas dans R. Cela illustre bien le caractère totalement artificiel de cette jauge. C'est une curiosité mathématique sur laquelle nous n'insisterons pas plus.