Tenseur électromagnétique - Définition

Équations de Maxwell

Les deux équations de Maxwell sans source ( et ) peuvent être combinées en une seule équation très simple, à savoir

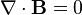
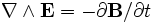
dF = 0,

qui découle elle-même du fait que F est déjà une dérivée extérieure, que la dérivée extérieure d'une dérivée extérieure est identiquement nulle.

Les deux équations impliquant la présence de charges, et , peuvent alors être réécrites sous la forme unifiée

,

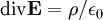
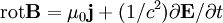
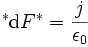
où j est le quadrivecteur du courant électrique.

Aspects mathématiques

Mathématiquement, le tenseur de Maxwell peut être vu comme la dérivée extérieure de A, ce que l'on peut noter sous la forme compacte

F = dA.

De ce fait, le tenseur de Maxwell peut être défini par un autre potentiel vecteur, A', défini par

,

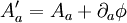
ou, plus simplement,

A' = A + dφ,

car la dérivée extérieure seconde d'une quantité est nulle par définition. Cette propriété, le fait que le tenseur de Maxwell soit défini à une transformation près du potentiel vecteur, est appelée invariance de jauge.