Théorème d'inversion locale - Définition

Démonstration

Étude d'un cas

Le théorème du point fixe permet de montrer l'inversion locale.

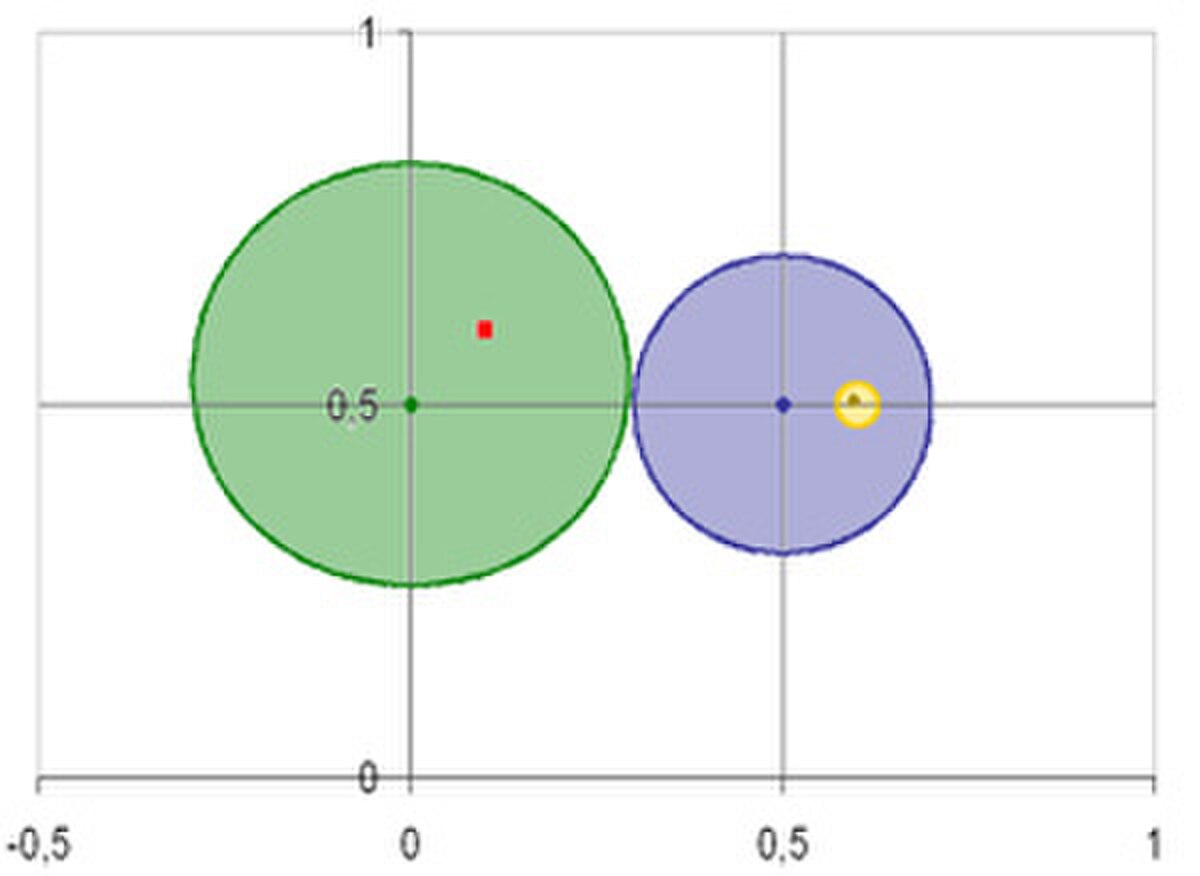
Pour comprendre le principe de la démonstration, illustrons là sur la fonction f de C dans C, qui à z associe z². L'objectif est de l'inverser au voisinage du point 1/2(1 + i). On peut considérer cette application comme étant celle de R² dans lui même, qui à (x, y) associe (x² - y², 2.x.y). Cette application est partout différentiable, et en particulier autour du point z₀ de coordonnées (1/2, 1/2). Le calcul de ma matrice jacobienne J_z donne :

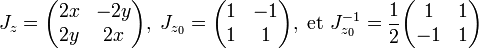
Sa différentielle est inversible au point z₀ et l'on note λ sa réciproque. L'objectif est de déterminer l'existence d'une application réciproque de f sur, par exemple le disque D de centre z₀ et de rayon 1/5. Cette zone est illustrée en bleu sur la figure de droite et son image en vert. Pour cela, il faut montrer qu'un point quelconque z₁ de la zone verte, possède un unique antécédent par f dans la zone bleue. Dans l'exemple on a choisi z₁ de coordonnées (0,1, 0,6), illustré en rouge. Cette question est relativement classique, une méthode pour y parvenir est d'utiliser le théorème du point fixe. Trois hypothèses doivent pour cela être vérifiées : l'ensemble considéré doit être complet, l'application g_y doit être d'un ensemble E dans lui même et elle doit être k-lipschitzienne avec k strictement plus petit que 1. L'espace C est complet, il ne reste plus qu'à construire la bonne fonction g. On la définit de D dans D par :

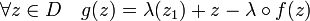
Au point z₀, comme λ désigne l'inverse de la différentielle de f en z₀, la différentielle de g est nulle. Il existe un voisinage sur lequel la différentielle de g est inférieure à 1/2, car g est continument différentiable. Le disque D est dans cette zone. Comme D est dans la zone contractante de g, cet ensemble est stable par g. L'image du disque D par g correspond à la zone jaune, une nouvelle itération donne une figure symbolisée par un point que la petitesse rend presque invisible sur la figure. En réitérant le processus, on obtient bien un point fixe et le théorème associé indique que ce point est unique. Si ce point fixe est noté ζ, il vérifie :

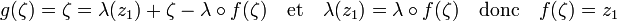
Dire que ζ est un point fixe de g revient exactement à dire qu'il est antécédent de z₁ par f, ce qui montre à la fois son existence et son unicité.

Existence d'une réciproque locale

L'approche précédente possède un avantage : nulle part il n'est fait usage de la dimension de l'espace vectoriel E contenant l'ouvert U, domaine de définition de f. En conséquence, la démonstration est naturellement valable sur un espace vectoriel normé complet quelconque, c'est-à-dire un espace de Banach. On utilise les mêmes notations que précédemment, f est une fonction de U dans un espace vectoriel normé F. Pour simplifier l'exposé, on cherche uniquement à montrer que f est inversible au point 0 et l'on suppose que f(0) = 0. Une fois ce cas traité, une simple translation permet de se ramener au cas général. La fonction f est supposée de classe C^p avec p strictement positif et la différentielle de f au point 0 est un isomorphisme continu dont la réciproque, notée λ, est aussi continue. On peut remarquer que l'on n'a pas supposé que F est un espace de Banach, mais comme les hypothèses supposent l'existence d'un isomorphisme bicontinu de E dans F, F est nécessairement un espace de Banach.

Soit φ l'application de U dans F, qui à x associe x - λ.f(x). En 0, l'application φ possède une différentielle nulle et, comme cette différentielle est continue, il existe un réel strictement positif r tel que la boule ouverte B_r de centre 0 et de rayon r soit incluse dans U et tel que la norme de la différentielle de g soit toujours strictement inférieure à 1/2 sur cette boule.

L'objectif est de montrer que f est injective sur la boule de rayon ν et de centre 0 et notée B_ν. L'application λ est continue, soit m sa norme, on définit ν comme étant un réel strictement positif et plus petit que r/(2.m). Si y est un point de B_ν, λ.y est de norme strictement inférieure à r/2. On construit la fonction φ_y de B_r dans elle même, où y est un point de B_ν :

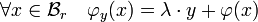
L'application φ_y est bien à valeur dans B_r car la norme de λ.y est inférieure à r/2, tout comme celle de φ(x). L'inégalité des accroissements finis montre que φ est 1/2-lipschitzienne et par voie de conséquence φ_y aussi car φ_y est une translation de φ. Le théorème du point fixe montre l'existence et l'unicité d'un point fixe de φ_y sur B_r, ce qui est équivalent à dire que f est bijective de B_ν dans son image.

Régularité de la réciproque

Il s'agit maintenant de montrer que la réciproque de f est de classe C^p. On note V l'image de B_ν par f. Soit y₁ et y₂ deux points quelconques de V et x₁, x₂ leurs antécédents. La continuité s'obtient à en remarquant que φ est 1/2 lipschitzien et :

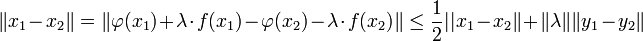
Ce qui s'écrit encore :

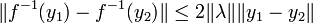
Montrons que la réciproque de f est différentiable sur V. Soit y un point de V et k un vecteur de F tel que y + k soit aussi élément de V. On note x + h l'image de y + k par la réciproque de f :

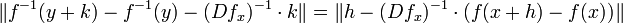
On remarque que la différentielle est supposée ici inversible non plus uniquement en x₀ mais sur un voisinage de x₀. L'ensemble des isomorphismes inversibles continus forment un ouvert. Pour s'en rendre compte, il suffit de remarquer que si β est un morphisme de petite norme et si α est un isomorphisme bicontinu, α + β s'écrit encore α(Id + α^-1β) qui est le produit de deux isomorphismes bicontinus. Pour le deuxième, il suffit d'utiliser un développement en série entière pour s'en rendre compte. La série est convergente si la norme de β est strictement plus petite que celle de l'inverse de α :

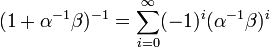
Un développement limité de la fonction f montre que :

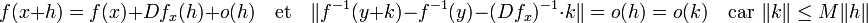
Où M est un majorant de la norme de la différentielle de f sur B_ν. Un tel majorant existe car φ est contractante sur B_ν et f(x) = λ^-1.(x - φ(x)).

Il reste encore à montrer que la réciproque de f est de classe C^p. La différentielle de la réciproque de f est la composée de la fonction f ^-1 par l'inverse de la différentielle de f. La fonction inverse est infiniment différentiable, f est de classe C^p et la réciproque de f est continue, on en déduit que la réciproque de f est de classe C¹. De proche en proche, on vérifie que la réciproque de f est de classe C^p.