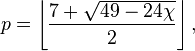Théorème des quatre couleurs - Définition

Conséquences

Algorithmiques

Déterminer si un graphe peut être ou non coloré en 2 couleurs est très facile : techniquement, il suffit de colorer arbitrairement un sommet de chaque composante connexe avec une couleur et ensuite de propager cette décision en colorant les sommets voisins avec l'autre couleur et ainsi de suite. Si l'on rencontre un sommet encore non coloré voisins de deux sommets de couleur différentes alors le graphe ne peut être biparti. C'est un problème soluble en temps polynomial.
En revanche, déterminer si un graphe peut être ou non coloré en k couleurs pour k>3 est un problème NP-complet. La preuve de Appel et Haken donne un algorithme pour colorer tout graphe planaire avec le minimum de couleur possible (donc au-plus quatre couleurs) en temps quadratique.

Pratiques

D’autres problèmes plus pratiques peuvent se réduire à la résolution de coloration de graphe, la solution peut alors être appliquée pour améliorer l'organisation de tâches.

• Affecter des fréquences différentes à des cellules voisines dans un réseau de téléphone mobile GSM.
• Organiser un examen suivant les matières que doit passer chaque étudiant. Comment mettre en parallèle plusieurs épreuves sans léser un candidat ?
• Optimiser l'utilisation des machines de travail. Comment mettre en parallèle des fabrications utilisant plusieurs machines ?
• Problème d'incompatibilité. Comment faire cohabiter des personnes ou animaux en tenant compte de leur incompatibilité ?

Cas du coloriage de cartes

S'agissant du coloriage des cartes elles-mêmes, le théorème a en fait un intérêt limité. Par exemple, si on souhaite dessiner une carte du monde en attribuant des couleurs différentes aux pays limitrophes :

• D'une part, on sera gêné par la présence de la mer. Soit il faut lui attribuer une couleur comme si c'était un pays — mais ce serait trompeur — soit il faut lui réserver une couleur supplémentaire.
• D'autre part, le théorème parle bien de régions connexes. L'oblast de Kaliningrad suffit à montrer que ce n'est pas forcément le cas des pays.

Généralisations du théorème des quatre couleurs

Classes de graphes plus générales que les graphes planaires

On voit que l'énoncé classique du théorème des quatre couleurs n'est bien sûr pas une caractérisation des graphes dont le nombre chromatique est inférieur ou égale à 4 puisque le K_3,3 n'est pas planaire mais est biparti. D'autre part, pour des raisons de complexité algorithmique, il ne peut exister de caractérisation simple des graphes k-colorables pour k fixé supérieur à 3. Le théorème des quatre couleurs se généralise aux graphes sans mineur K₅, puisque le nombre chromatique de ces graphes vaut au plus 4 (et c'est une des motivations de la conjecture d'Hadwiger). Une généralisation plus forte encore a été donnée récemment par Guenin :

• les graphes sans mineur impair K₅ sont colorables avec seulement 4 couleurs.

(Un mineur est dit impair si les opérations de suppressions et de contractions des arêtes s'effectuent uniquement sur une coupe du graphe. Un graphe contient un mineur impair K₅ s'il contient un K₅ dont on a remplacé les dix arêtes par dix chemins de longueur impairs.)

Ces résultats plus forts sont basés sur des preuves utilisant le théorème des quatre couleurs lui-même, par conséquent ils n'en apportent pas de nouvelle démonstration.

Surfaces plus générales que le plan

En recollant les flêches simples et doubles ensemble (respectivement), on obtient un tore avec sept régions se touchant six à six ; ainsi, sept couleurs sont nécessaires

Cette image montre le résultat du collage précédent.

On peut aussi considérer le problème du coloriage de cartes tracées sur des surfaces autres que le plan. Sur la sphère, le problème est le même (pour le voir, il suffit de retirer un point de la sphère intérieur à l'une des régions, et d'effectuer une projection stéréographique). Pour des surfaces fermées de genre positif, le nombre de couleurs nécessaires dans le pire des cas, p, dépend de la caractéristique d'Euler de la surface, χ, selon la formule

où les crochets extérieurs désignent la fonction partie entière.

Pour une surface orientable de genre g, cela revient à

(Eric Weisstein, Map coloring (en)).

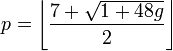
Cette formule fut conjecturée par Heawood en 1890 et prouvée par Ringel et Youngs en 1968. On remarquera que pour g=0, elle redonne le théorème des quatre couleurs, mais bien sûr, les preuves précédentes ne s'appliquent qu'au cas où g>0.

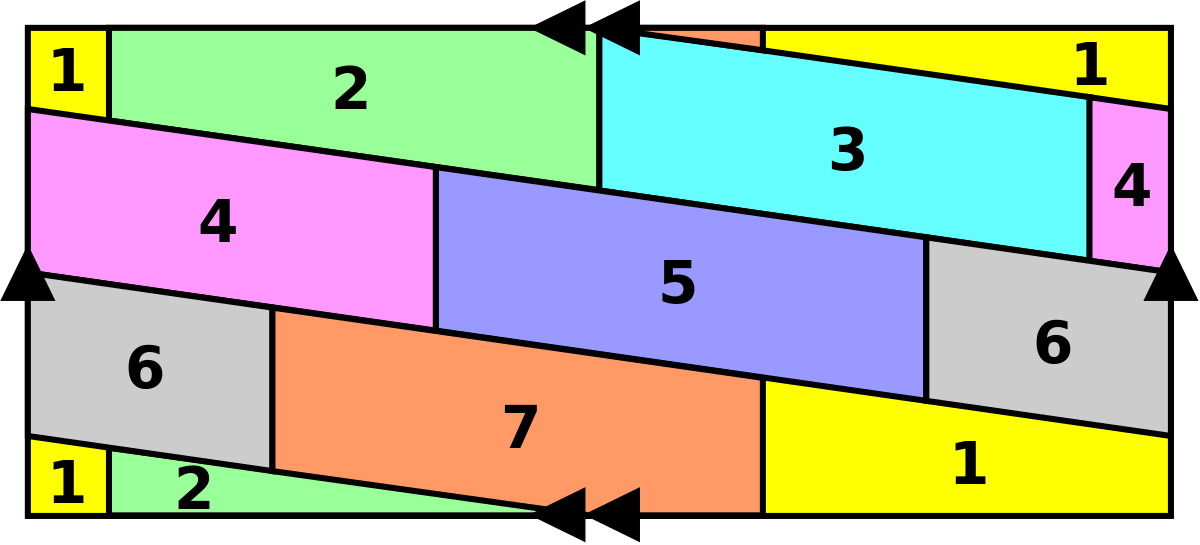
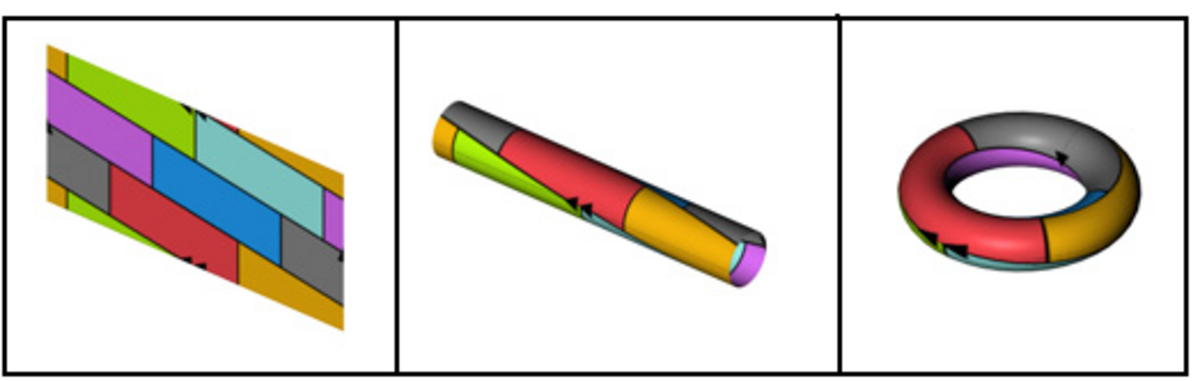
Par exemple, le tore a une caractéristique d'Euler χ = 0 (et est de genre g = 1 : un tore n'a qu'un "trou") et donc p = 7 ; 7 couleurs suffisent donc pour colorer n'importe quelle carte sur le tore, et l'exemple de la figure montre que cela peut être nécessaire ; des exemples analogues permettent de montrer que la valeur de la conjecture de Heawood est la plus petite possible.

Il n'y a pas de généralisation dans l'espace car tous les graphes, et en particulier le graphe complet, sont plongeables dans l'espace 3D, en d'autres termes, en utilisant n tiges flexibles, il est possible de les arranger pour que chacune touche toutes les autres, et donc n peut être choisi aussi grand qu'on veut, sans qu'apparaisse un "théorème des n couleurs".