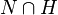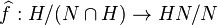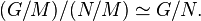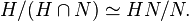Théorèmes d'isomorphisme - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, les trois théorèmes d'isomorphisme fournissent l'existence d'isomorphismes dans le cadre de la théorie des groupes.
Ces trois théorèmes d'isomorphisme sont généralisables à d'autres structures que les groupes. Voir notamment à Algèbre universelle.
Premier théorème d'isomorphisme
Le premier théorème d'isomorphisme affirme qu'étant donné un morphisme de groupes
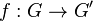
Intuitivement, quotienter un groupe G par un sous-groupe H revient à « annuler » les éléments de H. En quotientant par le noyau de f, on fait donc en sorte que f(x) = 1 ne soit vrai que pour x = 1, ce qui est équivalent à l'injectivité de f.
Pour pouvoir parler de morphisme de groupes
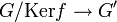
Proposition — Soient G et G' deux groupes et soit
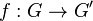
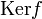
Notons

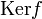
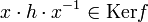
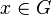
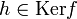
On a
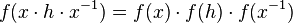
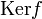
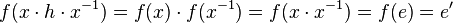
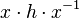
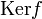
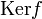
Le fait que
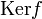
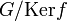
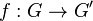
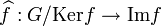
On peut maintenant énoncer le théorème.
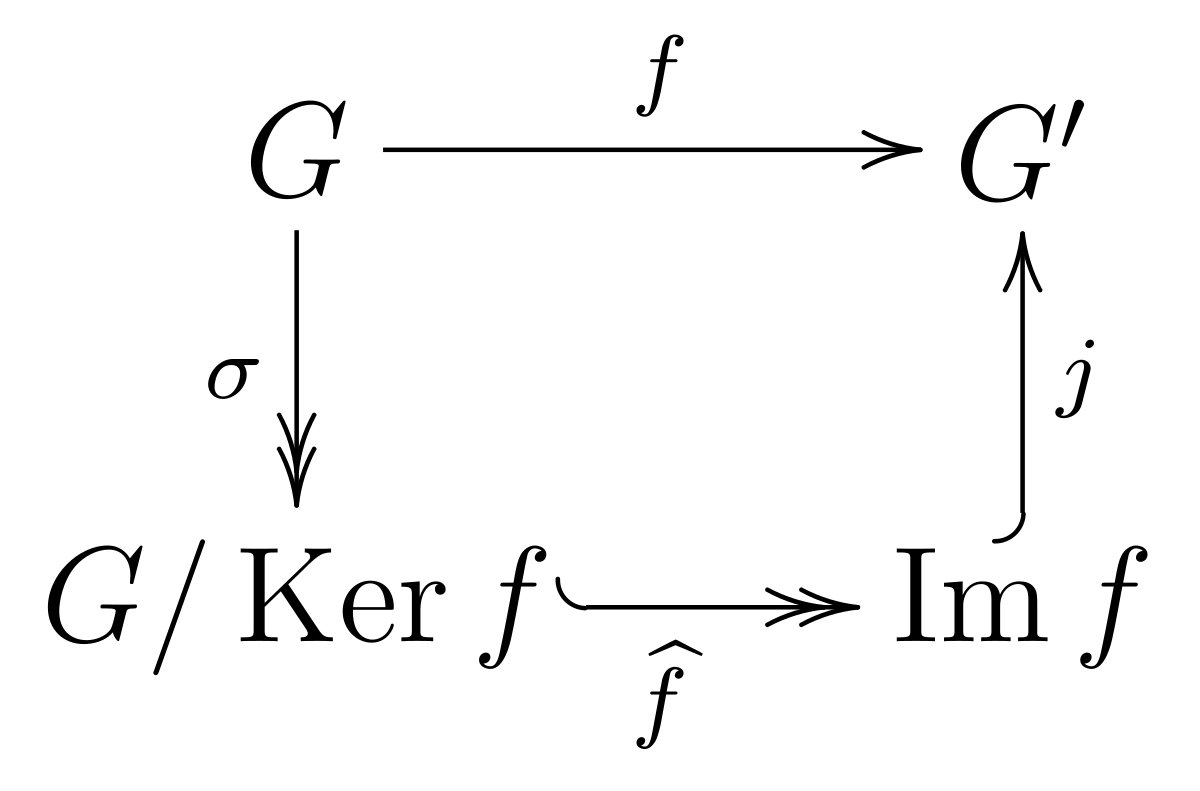
Premier théorème d'isomorphisme — Soient G et G' deux groupes, et soit
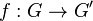
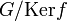
Notons H le noyau de f. On définit
-
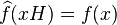
- La fonction
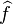
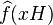
En effet, si
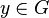
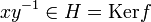
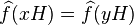
- Par définition de la loi de groupe quotient,
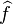
- Le morphisme
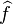
pour tout
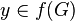
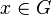
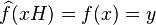
- Le morphisme
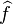
En effet, soit xH un élément de son noyau. Alors
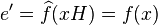
Une autre formulation possible du théorème précédent est que le morphisme f se factorise par la surjection et l'injection canoniques, c'est-à-dire que le diagramme qui suit est commutatif.
Troisième théorème d'isomorphisme
Troisième théorème d'isomorphisme — Soient G un groupe, N et M deux sous-groupes normaux de G. Alors N / M est alors un sous-groupe normal de G / M et on a l'isomorphisme suivant :
Deuxième théorème d'isomorphisme
Deuxième théorème d'isomorphisme — Soient G un groupe, N un sous-groupe normal de G et H un sous-groupe de G. Alors
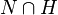
- Pour pouvoir parler du groupe HN / N, il faut d'abord montrer que HN est un groupe et que N en est un sous-groupe normal.
Soient hn et h'n' deux éléments de HN. On a hnh'n' = hh'(h' − 1nh')n', avec
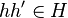
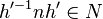
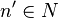
D'autre part, on a les inclusions de groupes
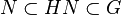
- Pour établir l'isomorphisme, nous allons utiliser le premier théorème d'isomorphisme.
On dispose d'un morphisme injectif
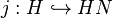
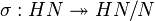
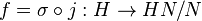
- Le morphisme f est surjectif.
En effet, soit
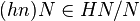
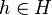
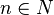
- Le noyau de f est
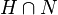
En effet, f(h) = hN est l'élément neutre N de HN / N si, et seulement si, h est dans N. Comme h est déjà dans H, cela revient à dire que h est dans
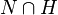
- Le premier théorème d'isomorphisme assure alors que