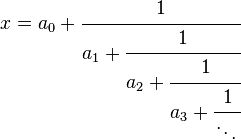Tribu de Lebesgue - Définition

Ensembles mesurables non boréliens

En mettant côte à côte le résultat de cardinalité qui précède et celui selon lequel la tribu borélienne de est équipotente à (voir la section « Un résultat de cardinalité » de l'article « Tribu engendrée »), on en déduit l'existence d'ensembles mesurables qui ne sont pas boréliens. Dit autrement, la mesure de Borel-Lebesgue n'est pas complète, et est donc distincte de la mesure de Lebesgue.

Des exemples de mesurables non boréliens étaient déjà connus de Lebesgue en 1905. En 1927, Nikolaï Luzin explicite un exemple particulièrement simple : si on considère T l'ensemble des réels ayant un développement en fraction continue de la forme

dans lequel la suite possède une sous-suite croissante pour la relation de divisibilité, l'ensemble T est mesurable (et même analytique) mais n'est pas borélien.

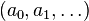
Généralisation aux variétés

Le concept se généralise aux variétés M de classe au moins . On définit une partie Lebesgue-mesurable de M comme une partie A qui vérifie la condition suivante :

pour toute carte de M, est mesurable.

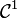
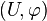
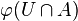
Lorsqu'on considère une partie A d'une sous-variété N de M, on prendra garde à ne pas confondre les notions de mesurabilité de A comme partie de N ou comme partie de M. Dès que N est de dimension strictement plus faible que M, tout est mesurable comme partie de M (car négligeable) mais ne l'est pas nécessairement comme partie de N.