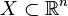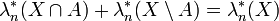Tribu de Lebesgue - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un ensemble Lebesgue-mesurable (qu'on abrège souvent en mesurable) est une partie de l'espace

Définition
Comme exposé à l'article mesure de Lebesgue, cette mesure sur



Cardinalité de la tribu de Lebesgue
Proposition — Le cardinal de la tribu de Lebesgue sur


Preuve :
Pour
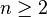
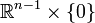

Pour n = 1 il faut chercher un exemple un peu moins évident. L'ensemble triadique de Cantor apporte la réponse : c'est un ensemble compact donc borélien, de mesure nulle, et pourtant en bijection avec

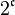


Caractérisation des mesurables de l'espace n-dimensionnel
Du point de vue de la complétion de la tribu de Borel
Les parties mesurables de

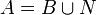
La variante suivante peut être utile : A est mesurable si et seulement si il peut être écrit sous la forme :
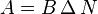
Du point de vue de la mesure extérieure
Dans cette section, on note
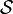
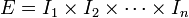

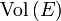
Pour
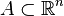
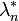
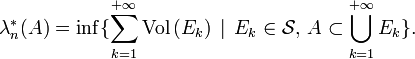
Cette caractérisation est due à Carathéodory, la caractérisation originelle par Lebesgue est la suivante :
Théorème — Soit
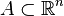
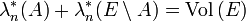
Il est facile de voir que le réel
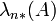
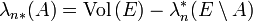
Pour des ensembles non bornés, on peut écrire un énoncé analogue au précédent, en faisant intervenir une suite de pavés remplissant l'espace :
Généralisation de l'énoncé précédent — Soit
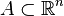
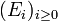

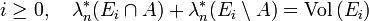
Ensembles non mesurables
La cardinalité ne permet pas de déterminer si la tribu de Lebesgue de


On connaît des exemples d'ensembles non-mesurables. Un des plus simples est l'ensemble de Vitali, inventé en 1905 par Giuseppe Vitali : un ensemble de représentants des classes de
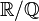
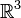
Ces deux exemples font appel à l'axiome du choix. Ce n'est pas fortuit. L'existence du modèle de Solovay (en), publié par Robert M. Solovay en 1970, montre en effet que dans la théorie des ensembles ZF sans axiome du choix, on ne peut espérer prouver l'existence d'ensembles non mesurables (et ce d'ailleurs même en supposant l'axiome du choix dépendant).