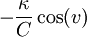Tube (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie, un tube est une surface orientée et paramétrée de
Paramétrage
Supposons que l'arc c soit sans point d'inflexion et paramétré par l'abscisse curviligne. Le plan normal en c(s) est le plan vectoriel orthogonal au vecteur vitesse τ = c', c'est-à-dire le plan vectoriel engendré par :
- la normale unitaire ν(s), l'unique vecteur unitaire positivement colinéaire à τ'(s),
- et la binormale
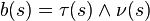
Le cercle euclidien de rayon r de centre c(s) tracé dans le plan normal est simplement paramétré par :
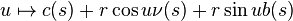
En faisant varier s, on obtient un paramétrage du tube de rayon r autour de c :
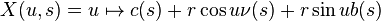
Si la courbe c a un rayon de courbure constamment inférieur à r, le paramétrage obtenu est régulier. Il s'agit même d'un plongement.
Propriétés métriques
Les propriétés métriques des tubes sont résumés dans le tableau suivant :
| Propriété métrique | Résultat |
|---|---|
| Première forme fondamentale |
|
| Forme d'aire |
|
| Seconde forme fondamentale |
|
| Courbures principales |
|
La courbe c est supposée paramétrée par longueur d'arc. Pour aborder les questions métriques des tubes, il est important de se rappeler les lois de dérivation sur les repères de Frenet :
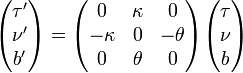
où κ est la courbure et θ est la torsion. Ces lois dérivations interviennent directement dans le calcul des dérivées premières de X(s,v) par rapport aux paramètres s et v, nécessaire pour exprimer la première forme fondamentale :
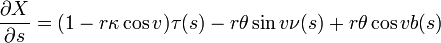
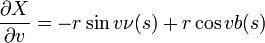
On pose alors :
On suppose que cette quantité est strictement positive (c'est la condition pour que X soit un plongement). La première forme fondamentale s'écrit :
![\mathrm{d}X^2={\left\|\frac{\partial X}{\partial s}\right\|}^2 \mathrm{d}s^2+2\left\langle\frac{ \partial X}{\partial s}\Bigg|\frac{\partial X}{\partial v}\right\rangle\mathrm{d}s\cdot\mathrm{d}v+{\left\|\frac{\partial X}{\partial v}\right\| }^2 \mathrm{d}v^2=\left[C^2+r^2\theta^2\right]\mathrm{d}s^2+2r^2\theta \mathrm{d}s\cdot\mathrm{d}v+r^2\mathrm{d}v^2](https://static.techno-science.net/illustration/Definitions/autres/2/2f0426016577cc813a5b7c8f7af231e0_ea48927dfbb1b9a32f81e675919215aa.png)
La forme volume sur la surface X s'écrit :
![\omega=\sqrt{\left[C^2+r^2\theta^2\right]\cdot r^2-\left[r^2\theta\right]^2}\mathrm{d}s\wedge \mathrm{d}v=rC \mathrm{d}s\wedge \mathrm{d}v](https://static.techno-science.net/illustration/Definitions/autres/3/3087439a80e6d741f1d557e443374312_eab33674b3f5d13d31df587801d48e19.png)
De suite, l'aire A de la surface
![\{X(s,v)\}_{v\in S^1,s\in [0,L]}](https://static.techno-science.net/illustration/Definitions/autres/e/e63876f5001a07116beee8091f9ef1c1_f419e16b742849c2efbd20e32ad74029.png)
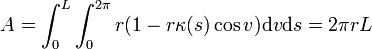
Le calcul de la seconde forme fondamentale requiert la connaissance du vecteur unitaire normal et des dérivées partielles secondes de X(s,v) par rapport à s et à v :
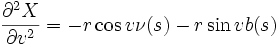
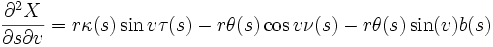
![\begin{align}\frac{\partial^2 X}{\partial u^2} &= r\left[\kappa(s)\theta(s)\sin v-\kappa'(s)\cos v\right]\tau(s)\\ &+\left[\kappa(s)C(s,v)-r\theta'(s)\sin v-r\theta(s)^2\cos(v)\right]\nu(s)+r\left[\theta'(s)\cos v -\theta(s)^2\sin v\right]b(s)\end{align}](https://static.techno-science.net/illustration/Definitions/autres/9/935430a4bd59603f49918160970d84c2_64586bde53d4e4829b52a42a4b541e8e.png)
La seconde forme fondamentale de X s'écrit donc :
![\left[-\kappa(s)\cos v C(s,v)+r\theta(s)^2\right]\mathrm{d}s^2+r\theta(s)\mathrm{d}s\cdot \mathrm{d}v+r\mathrm{d}v^2](https://static.techno-science.net/illustration/Definitions/autres/5/544f28a5dd4061ddd7dc52ea0b80ade9_b87f6be912239436a8ca01d4947c2af2.png)
Les courbures principales sont les valeurs propres de l'endomorphisme symétrique :
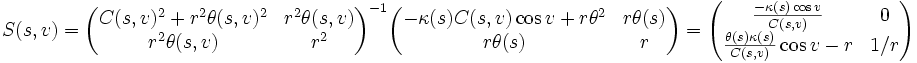
Elles sont donc :
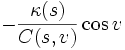

Exemples

On ne saurait s'empêcher de citer les deux exemples élémentaires suivants :
- Si c est le paramétrage d'une droite affine, id est, c(s) = sV + c(0) avec V un vecteur unitaire de R3, alors le tube de rayon r autour de c est le cylindre de rayon r et d'axe de symétrie la droite
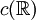
- Si c est le paramétrage d'un cercle de rayon R > r, id est c(s) = P + RcossV + RsinsW où V et W sont des vecteurs unitaires orthogonaux, le cylindre de rayon r autour de c est un tore, d'axe de symétrie de rotation
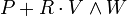
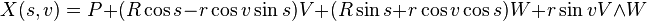
- Un autre exemple est celui de l'hélicoïde cerclé.
La notion de tube ne doit être considérée comme une figure mathématique abstraite. Elle est seulement la représentation paramétrée idéalisée de nombreux objets réels, comme les tubes fluorescents, les pneus, ou la couleuvre.
![\mathrm{d}X^2=\left[C^2+r^2\theta^2\right]\mathrm{d}s^2+2r^2\theta\mathrm{d}s\cdot\mathrm{d}v+r^2\mathrm{d}v^2](https://static.techno-science.net/illustration/Definitions/autres/1/1c1d55df4f3a6422e4ccc4c5734a83f6_7bbf5a7a79fb667f5482632b31381cae.png)
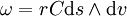
![\left[-\kappa\cos v C+r\theta^2\right]\mathrm{d}s^2+r\theta \mathrm{d}s\cdot\mathrm{d}v+r\mathrm{d}v^2](https://static.techno-science.net/illustration/Definitions/autres/b/b745be1d7253ec3e3fef3c77f492e3df_b8b113eab215264bdce5a4dc075b2832.png)