Zonoèdre - Définition

Dissection des zonoèdres

Bien qu'il ne soit pas généralement vrai qu'un polyèdre quelconque puisse être disséqué en un autre polyèdre quelconque de même volume (voir le troisième problème de Hilbert), il est connu que deux zonoèdres quelconques de mêmes volumes peuvent être disséqués l'un dans l'autre.

Types de zonoèdres

Nous avons déjà vu que tout prisme sur un polygone régulier avec un nombre pair de côtés forme un zonoèdre. Ces prismes peuvent être formés si toutes les faces sont régulières : deux faces opposées sont égales au polygone régulier à partir duquel le prisme a été formé, et celles-ci sont connectées par une suite de faces carrées. Les zonoèdres de ce type sont le cube, le prisme hexagonal, le prisme octogonal, le prisme décagonal, le prisme dodécagonal, etc.

En plus de cette famille infinie de zonoèdre à faces régulières, il existe trois solides d'Archimède, toutes les omnitroncatures des formes régulières :

• L'octaèdre tronqué, avec 6 carrés et 8 faces hexagonales. (Tétraèdre omnitronqué)
• Le grand rhombicuboctaèdre, avec 12 carrés, 8 hexagones et 6 octogones. (Cube omnitronqué)
• Le grand rhombicosidodécaèdre, avec 30 carrés, 20 hexagones et 12 décagones. (Dodécaèdre omnitronqué)

En plus, certains solides de Catalan (duaux des solides d'Archimède) sont encore des zonoèdres :

• Le dodécaèdre rhombique qui est le dual du cuboctaèdre.
• Le triacontaèdre rhombique qui est le dual de l'icosidodécaèdre.

Autres polyèdres avec toutes les faces rhombiques :

• L'icosaèdre rhombique
• Le rhomboèdre
• L'ennéacontaèdre rhombique

zonoèdre		face régulière	face uniforme	arête uniforme	sommet uniforme	Cellule uniforme remplissage d'espace
Cube 4.4.4	Cube	oui	oui	oui	oui	oui
Prisme hexagonal 4.4.6		oui	non	non	oui	oui
2n-prisme (n >3) 4.4.2n		oui	non	non	oui	non
Octaèdre tronqué 4.6.6	Octaèdre tronqué	oui	non	non	oui	oui
Grand rhombicuboctaèdre 4.6.8	Cuboctaèdre tronqué	oui	non	non	oui	non
Grand rhombicosidodécaèdre 4.6.10		oui	non	non	oui	non
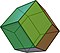
Dodécaèdre rhombique V3.4.3.4		non	oui	oui	non	oui
Triacontaèdre rhombique V3.5.3.5		non	oui	oui	non	non
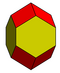
Dodécaèdre rhombo-hexagonal		non	non	non	non	oui
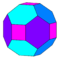
Dodécaèdre rhombique tronqué		non	non	non	non	non