Principe des tiroirs - Définition
Le principe des tiroirs déclare que si n chaussettes occupent m tiroirs, et si n > m, alors au moins un tiroir doit contenir strictement plus d'une chaussette. Une autre formulation serait que m tiroirs ne peuvent contenir strictement plus de m chaussettes avec une seule chaussette par tiroir; ajouter une autre chaussette obligera à réutiliser un des tiroirs.
Mathématiquement, le principe de tiroirs peut s'énoncer ainsi :
- Si E et F sont deux ensembles finis, tels que card(E) > card(F) et si f : E→F est une application de E dans F, alors il existe un élément de F qui admet au moins deux antécédents par f.
Ou encore :
- Si E et F sont deux ensembles finis, tels que card(E) > card(F) et si f : E→F est une application de E dans F, alors f n'est pas injective; autrement dit, il n'existe pas d'application injective de E dans F.
Appellation
La première version du principe fut énoncée par Dirichlet en 1834 sous le nom de Schubfachprinzip (" principe du tiroir "), suite à une observation de ses chaussettes dans sa commode. Dans certains pays comme la Russie, ce principe s'appelle le principe de Dirichlet (à ne pas confondre avec le principe du maximum pour les fonctions harmoniques, du même nom). Ce principe est aussi appelé principe des tiroirs de Dirichlet-Schläfli, ou encore principe des boîtes, ou par traduction littéraire de l'anglais le principe des trous de pigeons. Dans cette dernière image, on remplace chaussette par œuf de pigeon et tiroir par nid de pigeon !
Applications
Bien que le principe des tiroirs semble être une observation totalement insignifiante, il peut être employé pour démontrer des résultats inattendus.
Par exemple, il doit y avoir au moins deux personnes à Dallas au Texas avec le même nombre de cheveux sur leur tête. Démonstration: une tête normale a environ 150 000 cheveux et il est raisonnable de supposer que personne n'a pas plus de 1 000 000 de cheveux sur la tête. Il y a plus de 1 000 000 personnes à Dallas. Si nous associons à chaque nombre de cheveux sur une tête un tiroir, et si nous plaçons chaque habitant de Dallas dans le tiroir correspondant à son nombre de cheveux sur la tête, alors d'après le principe des tiroirs, il y a nécessairement au moins deux personnes ayant exactement le même nombre de cheveux sur la tête à Dallas ! Évidemment, le résultat reste vrai pour n'importe quelle mégalopole.
Donnons un autre exemple d'application du principe des tiroirs dans la situation où il y a cinq personnes qui veulent jouer au rugby, mais seulement quatre équipes. Ce ne serait pas un problème si chacune des cinq personnes ne refusait pas de jouer dans une équipe avec l'une quelconques des quatre autres. Pour montrer qu'il n'y a aucun moyen pour que chacune des cinq personnes jouent au rugby, nous appliquons le principe des tiroirs qui indique qu'il est impossible de répartir cinq personnes dans quatre équipes sans mettre deux joueurs dans la même équipe. Puisque les joueurs refusent de jouer dans la même équipe, tout au plus quatre joueurs pourront jouer.
Approximation d'un réel
Soit un réel x et un entier naturel n. Pour tout réel y, on définit {y} la partie fractionnaire de y, id est y − E(y). On dispose de (n + 1) éléments de [0,1] : 0, {x},
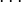
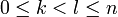
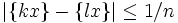
- | (k − l)x − q | < 1 / n donc
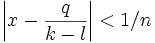
Généralisations
Une version généralisée de ce principe déclare que, si n objets discrets occupent m récipients, alors au moins un récipient doit contenir au moins
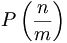
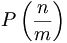
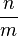
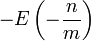
Le principe des tiroirs est un exemple d'argument de dénombrement. Ce principe peut être appliqué à de nombreux problèmes sérieux, y compris ceux qui impliquent des ensembles infinis qui ne peuvent pas être mis en correspondance univoque. En approximation diophantienne, l'application quantitative du principe montre l'existence de solutions entières d'un système d'équations linéaires et ce résultat porte le nom de lemme de Siegel.

















































