Relation ternaire interne - Définition
Une relation ternaire interne dans un ensemble associe des éléments de cet ensemble à des couples formés d’éléments de ce même ensemble.
Définitions
Formellement, une relation ternaire interne est une correspondance dont l’ensemble de départ est le carré cartésien de l’ensemble d’arrivée.
En d’autres termes, une relation ternaire interne

- un ensemble de départ, E×E ;
- un ensemble d’arrivée, E ;
- et un graphe G, inclus dans E 3, donc formé de triplets d’éléments de E.
Si x, y et z sont trois éléments de E , nous pouvons écrire que z est image par

- ( x , y , z ) ∈ G (notation ensembliste)
- ( x , y , z )
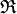
-
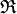
- ( x , y )

Nous utiliserons dans la suite cette dernière notation.
Cas particuliers :
- Une opération interne est une relation ternaire interne qui est aussi une fonction.
- Une loi de composition interne est une relation ternaire interne qui est aussi une application.
Exemples
- La relation d'équidistance dans un espace métrique, c'est-à-dire muni d'une distance d :
-
- Un point A est équidistant de deux points B et C ssi d ( A , B ) = d ( A , C )
- Ce n'est ni une opération, ni une loi de composition interne.
- L' exponentiation Exp définie par : [ ( x , y ) Exp z ] ⇔ [ z = x y ]
- C'est une opération interne dans
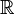
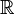
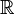
- La différence de deux ensembles Diff : [ ( A , B ) Diff C ] ⇔ [ C = A \ B ] .
- C'est une loi interne dans l'univers des ensembles, ou dans l'ensemble des parties d'un ensemble.
- Parmi les êtres humains, la relation " sont respectivement père et mère de " n'est ni une opération, ni une loi interne : un couple peut être sans enfants ou en avoir plusieurs.
- Les quatre " opérations " de notre enfance (addition, soustraction, multiplication et division) sont bien des opérations car leur résultat, quand il est défini, l'est toujours sans ambiguïté.
Propriétés
Soit un ensemble E muni d’une relation ternaire interne

- Les propriétés suivantes s’appliquent évidemment aussi aux lois de composition internes, mais sous une forme simplifiée par l'emploi d'une notation fonctionnelle (z = f ( x, y ) ou z = x
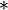
- Attention : un couple peut très bien avoir plusieurs images par

- La liste de propriétés qui suit n’est pas exhaustive.
Existence d’éléments remarquables
-


- ou :
-
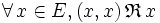
-


- ou :
-
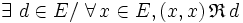
-


- ou :
-
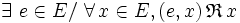
-


- ou :
-
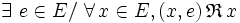
-

-


- ou :
-
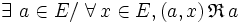
-


- ou :
-
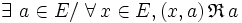
-

-

-

-

-

-

-

Régularité et propriétés apparentées
-


- ou :
-
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( x , y ) \mathfrak{R} \, t ] \Rightarrow [ z = y ] \,](https://static.techno-science.net/illustration/Definitions/autres/5/549f28404efae22a121c59b8bbce5754_fdb4e638d59969bf29cf55ae32fde48b.png)
-


- ou :
-
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( y , z ) \mathfrak{R} \, t ] \Rightarrow [ x = y ] \,](https://static.techno-science.net/illustration/Definitions/autres/0/03287cd94ae9ea382465cbba1b588fae_3e4e0c310f3d2e5a6634132075e5170e.png)
-

-


- ou :
-
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( y , x ) \mathfrak{R} \, t ] \Rightarrow [ z = y ] \,](https://static.techno-science.net/illustration/Definitions/autres/7/7b8e06ab3a08249344708d75e66aabf3_bba032b92809e634cf0df8c64b4abfe5.png)
Associativité et propriétés analogues
-

-

-

Autres propriétés
-


- ou :
-
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \mathfrak{R} \, z ] \Rightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](https://static.techno-science.net/illustration/Definitions/autres/3/38f24df8c6644fc316deef9c9a46eecb_d7c3c74b9e868fce2d556df5e695246c.png)
Relation ternaire opposée
Définition et exemples
Soit un ensemble E muni d'une relation ternaire interne

La relation ternaire opposée à


Par exemple, la relation opposée à l' exponentiation Exp définie par : [ ( x , y ) Exp z ] ⇔ [ z = x y ] est la relation z = y x .
Un autre exemple est la différence de deux ensembles Diff : [ ( A , B ) Diff C ] ⇔ [ C = A \ B ] .
Sa relation opposée est définie par [ ( A , B ) (-Diff) C ] ⇔ [ C = B \ A ].
Ou encore, parmi les êtres humains, la relation " sont respectivement père et mère de " a pour opposée la relation " sont respectivement mère et père de ".
Propriétés
- Chaque relation ternaire interne a une relation opposée et une seule.
- Toute relation ternaire est l'opposée de son opposée.
- L'opposée d'une relation ternaire est une opération si et seulement si cette relation est une opération.
- L'opposée d'une relation ternaire est une loi de composition si et seulement si cette relation est une loi de composition.
- Une relation ternaire se confond avec son opposée si et seulement si elle est commutative.
Relations ternaires inverses
Définitions et exemples
Soit un ensemble E muni d'une relation ternaire interne

La relation ternaire inverse à gauche ( ou RTIG) de la relation

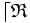
La relation ternaire inverse à droite ( ou RTID) de la relation

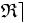
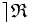
Pour clarifier ces notions reprenons l'exemple de l'exponentiation Exp.
- Sa RTIG est définie par : z = x 1/y ; autrement dit, c'est la racine y-ième de x;
- Sa RTID est définie par : z = log y x ; autrement dit, c'est le logarithme en base y de x.
Si

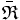
Exemples :
Ces exemples montrent qu'en général les RTI ne sont pas commutatives; sauf exception, elles n'ont donc pas elles-mêmes de RTI, seulement une RTIG et une RTID distinctes, la RTIG n'étant autre que la relation ternaire initiale, et la RTID l'opposée de la RTI.
Ainsi, la soustraction, non commutative, a pour RTIG l'addition et pour RTID la relation opposée à la soustraction. Cette dernière, par ailleurs, a pour RTID l'addition et pour RTIG la soustraction.
Propriétés
- Toute relation ternaire interne est la RTIG de sa RTIG, et la RTID de la RTID de sa RTID.
- La RTIG de l'opposée d'une relation ternaire est la RTID de cette dernière.
- La RTID de l'opposée d'une relation ternaire est la RTIG de cette dernière.
- La RTID de la RTIG d'une relation ternaire interne est la relation opposée à sa RTID.
- La RTID de la RTID d'une relation ternaire interne est la relation opposée à sa RTIG.
Dans les propriétés précédentes, des symétries apparaissent. Plus précisément, il est possible d'importer sur l'ensemble
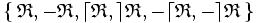

-

-

- Si

- Si

-

-

-

- Si

-

Exemples :
- (
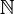
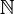
- de même, (


- (
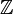
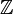
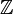
- de même, (


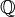
![\forall ( u , v , w , x , y , z ) \in E^{\, 6} , [ ( x , y ) \mathfrak{R} \, u \wedge ( u , z ) \mathfrak{R} \, w \wedge ( y , z ) \mathfrak{R} \, v ] \Rightarrow [ ( x , v ) \mathfrak{R} \, w ] \,](https://static.techno-science.net/illustration/Definitions/autres/9/940aee35b1f55538fe40ca42ff68d6ff_0c1b4645ac15809c37a0d2a416d2b0ef.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , x ) \mathfrak{R} \, y \wedge ( x , y ) \mathfrak{R} \, z ] \Rightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](https://static.techno-science.net/illustration/Definitions/autres/5/5c428cff4b1bfe141f5d15654aea89f1_8cd618d52072c0c017a010d7275983cd.png)
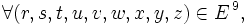
![[ ( x , y ) \mathfrak{R} \, z \wedge ( u , v ) \mathfrak{R} \, w \wedge ( x , u ) \mathfrak{R} \, r \wedge ( y , v ) \mathfrak{R} \, s \wedge ( z , w ) \mathfrak{R} \, t ] \Rightarrow [ ( r , s ) \mathfrak{R} \, t ] \,](https://static.techno-science.net/illustration/Definitions/autres/b/bc7737d69c6da100dc4200b465b62d96_49aebbcdf95c23a7b92d5d1ffc463d11.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) (-\mathfrak{R}) \, z ] \Leftrightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](https://static.techno-science.net/illustration/Definitions/autres/3/3d05487dc3bc76510b13dcc7fca10887_cf50c3e5108557a257504bef1f7800da.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \lceil \mathfrak{R} \, z ] \Leftrightarrow [ ( z , y ) \mathfrak{R} \, x ] \,](https://static.techno-science.net/illustration/Definitions/autres/2/2f55c9f753ba5ccc9a45a2bdf1279405_e920f8ad41cb38473fb820d7830a49ed.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \mathfrak{R} \rceil \, z ] \Leftrightarrow [ ( y , z ) \mathfrak{R} \, x ] \,](https://static.techno-science.net/illustration/Definitions/autres/7/74313d885ba31f7bd8bc08922c4ba37d_79d8d8ba15685404a3708b85f81ae1f8.png)

















































