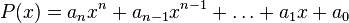Critère d'Eisenstein - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En mathématiques, le critère d'Eisenstein donne des conditions suffisantes pour qu'un polynôme soit irréductible sur $\mathbb{Q}\,$ (ou de la même façon irréductible sur $\mathbb{Z}\,$ ).

Considérons le polynôme suivant à coefficients entiers

Supposons qu'il existe un nombre premier $p\,$ tel que

$p\,$ divise chaque $a_i\,$ sauf $a_n\,$ ,
$p^2\,$ ne divise pas $a_0\,$

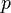
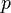
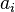
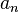
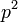
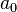
Alors $P(x)\,$ est irréductible.

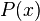
Exemples

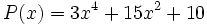
Considérons le polynôme $P(x) = 3x^4 + 15x^2 + 10\,$ .

Nous examinons différents cas pour les valeurs de $p\,$ suivantes

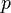
p = 2
2 ne divise pas 15, on ne peut pas conclure
p = 3
3 ne divise pas 10, on ne peut pas conclure
p = 5
5 divise 15, le coefficient de x², et 10 le coefficient constant. 5 ne divise pas 3, le coefficient dominant. En outre, 25 = 5² ne divise pas 10.
Ainsi, nous concluons grâce au critère d'Eisenstein que P(x) est irréductible.

Dans certains cas le choix du nombre premier peut ne pas être évident, mais peut être facilité par un changement de variable de la forme y = x + a, appelé translation.

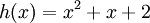
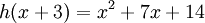
Par exemple considérons $h(x)=x^2 + x + 2\,$ . L'application du critère semble compromise puisque qu'aucun nombre premier ne divisera 1, le coefficient de x. Mais si nous translatons h (x) en $h(x + 3) = x^2 + 7x + 14\,$ nous voyons immédiatement que le nombre premier 7 divise le coefficient de x et de le coefficient constant et que 49 ne divise pas 14. Ainsi en translatant le polynôme nous l'avons fait satisfaire le critère d'Eisenstein.

Un autre cas connu est celui du polynôme cyclotomique d'indice un entier premier p, c’est-à-dire le polynôme

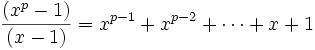
Ici, le polynôme satisfait le critère d'Eisenstein, dans une nouvelle variable y après une translation x = y + 1. Le coefficient constant est alors égal à p ; les autres coefficients sont divisibles par p d'après les propriétés des coefficients binomiaux $C_p^k\,$ (p! étant divisé par quelque chose n'impliquant pas p).

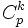
Démonstration basique

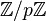
Considérons P(X) comme un polynôme modulo p; c’est-à-dire un polynôme dont les coefficients ont été réduits à des nombres du corps $\mathbb{Z}/p\mathbb{Z}\,$ . Il devient un polynôme de la forme c.Xⁿ où c est un nombre différent de 0. Puisque de tels polynômes se décomposent en produits de facteurs irréductibles de façon unique, toute factorisation de P (modulo p) ne doit faire intervenir que des monômes.

Maintenant si par l'absurde, P n'était pas irréductible comme polynôme à coefficients entiers, nous pourrions l'écrire sous la forme Q.R, et donc P modulo p sous la forme du produit de Q modulo p et R modulo p. Ces derniers devraient être des monômes, comme cela a été dit juste avant, ce qui signifierait que Q modulo p s'écrit sous la forme d. X ^k et R modulo p sous la forme e. X^{n – k} où c = d. e.

Enfin les conditions données sur Q modulo p de R modulo p impliqueraient que p ² divise a₀, ce qui serait contradictoire avec les hypothèses. En fait a₀ est égal à Q(0). R (0) et p divise les deux facteurs, d'après ce qui a été dit plus haut.