Hypercube magique - Définition
En mathématiques, un hypercube magique est la généralisation k-dimensionnelle d'un carré magique, d'un cube magique et d'un tesseract magique, c’est-à-dire, un nombre d'entiers arrangés dans un motif de taille n × n × n × ... × n tel que les nombres de chaque pile (le long de chaque axe) ainsi que des diagonales principales est égale à un nombre unique, ce que l'on appelle la constante magique d'un hypercube magique, noté
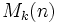
Si, de plus, les nombres de chaque section plane diagonale donnent aussi la constante magique de l'hypercube magique, l'hypercube est appelé un hypercube magique parfait ; autrement, il est appelé un hypercube magique semi-parfait. Le nombre n est appelé l'ordre de l'hypercube magique.
Les hypercubes à dimensions cinq, six, sept et huit d'ordre trois ont été construits par J. R. Hendricks. Marián Trenkler a démontré le théorème suivant : Un hypercube magique p-dimensionnel d'ordre n existe si et seulement si p > 1 et
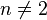
Le langage de programmation R inclut un module, library(magic), qui peut créer des hypercubes magiques de n'importe quelle dimension (avec n multiple de 4).