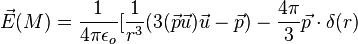Dipôle électrique d'une boule - Définition

Soit une boule, de rayon R, de polarisation uniforme,donc de moment dipôlaire . Le champ électrique créé par cette boule est le même que celui d'une sphère chargée en surface par une densité surfacique de révolution σ(θ) = Pcosθ.

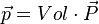
Champ et potentiel créés

Comme la distribution est à support compact , le champ au loin (r>>R) comme celui créé par le dipôle p.

Il est extraordinaire de constater que cela est vrai pour tout r > R !

Pour r < R , le champ est uniforme Eo = - P/3ε_o

Le diagramme électrique est donc évident à tracer.

Démonstration

On peut faire le calcul ; mais la démonstration la plus rapide est "bluffante" : la solution existe et est unique; il suffit donc de vérifier que div E = 0 et rot E = 0 , et que les conditions limite à l'infini sont réalisées ( c'est exact) et sur la sphère aussi ( E_ext - E_int = σ(P) / ε_o.n(P)) (c'est exact aussi).

Cas-limite R tendant vers zéro

On a, à ce moment-là , à représenter le petit volume V, où l'intégrale du champ vaut Vol.Eo = - P/3ε_o par -4π / 3.p. δ(r).

Au total ]