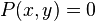Courbe algébrique - Définition

Une courbe algébrique est une courbe, le plus souvent plane, dont l’équation cartésienne peut se mettre sous forme polynômiale. Une courbe non algébrique est dite transcendante.

En géométrie algébrique, une courbe est une variété algébrique dont les composantes connexes sont toutes de dimension 1. En pratique, on se restreint souvent aux courbes projectives non-singulières et connexes.

Définition

Une courbe algébrique est plus formellement l’ensemble des points d’un espace géométrique dont les coordonnées cartésiennes sont solutions d’une équation algébrique.

L’espace géométrique considéré est le plus souvent le plan affine euclidien réel, mais il est possible :

- de recourir à des espaces de dimension supérieure à deux (espace ou hyperespace au lieu du plan) ;

- de se placer dans le cadre d’une autre géométrie qu’affine euclidienne (projective par exemple);

- de travailler avec un autre corps de base que celui des réels (en cryptographie par exemple, on utilise des plans sur des corps finis).

Nous nous limiterons cependant ici au cas du plan affine euclidien réel.

Les coordonnées cartésiennes d’un point M dans le plan sont deux nombres ( habituellement réels, mais cela peut dépendre du plan considéré ) appelés respectivement abscisse et ordonnée, et notés habituellement x et y. Ils désignent les valeurs des projections du point M sur deux axes orthogonaux du plan.

Une équation algébrique dans le plan est une équation qui peut être mise sous la forme :

où P( x, y ) désigne un polynôme irréductible de degré non nul des coordonnées cartésiennes x et y.

Ordre et classement

Le polynôme   P   ainsi associé à une courbe n’est pas unique; en fait, il n’est défini qu’à une constante multiplicative près : si   P   est associé à une courbe, alors tout polynôme   λ.P   où   λ   est un réel non nul lui est aussi associé. Cependant, tous ces polynômes sont du même degré, appelé ordre de la courbe algébrique.

Les courbes algébriques peuvent ainsi être classées suivant leur ordre n :

• pour   n = 1  , nous avons les rectiques ; ce sont en fait les droites ;
• pour   n = 2  , nous avons les coniques, ainsi appelées parce qu’il est possible de les obtenir comme intersection d’un cône et d’un plan; elles se répartissent en trois familles :

- les ellipses, dont le cercle;

- les hyperboles, dont l’hyperbole équilatère;

- et les paraboles.

• pour   n = 3  , nous avons les cubiques;
• pour   n = 4  , nous avons les quartiques;
• pour   n = 5  , nous avons les quintiques;
• pour   n = 6  , nous avons les sextiques;
• pour   n = 7  , nous avons les septiques;
• pour   n = 8  , nous avons les octiques, ou biquartiques;
• pour   n = 9  , nous avons les noniques, ou tricubiques;

• pour   n = 10  , nous avons les déciques, ou biquintiques;

• pour   n = 11  , nous avons les undéciques;
• pour   n = 12  , nous avons les duodéciques, ou triquartiques;

• au-delà, et même assez souvent à partir de l’ordre 9, on parle plutôt de " courbe algébrique d’ordre n " ...