Espace de Hilbert - Définition

Un espace de Hilbert est un espace de Banach (donc complet) dont la norme découle d'un produit scalaire ou hermitien par la formule . C'est la généralisation en dimension quelconque d'un espace euclidien ou hermitien.

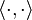
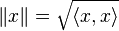
Théorème de M. Fréchet - J. von Neumann - P. Jordan

Un espace de Banach (respectivement espace vectoriel normé) est un espace de Hilbert (respectivement espace préhilbertien) ssi sa norme vérifie l'égalité

,

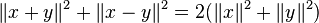
qui signifie que la somme des carrés de côtés d'un parallélogramme est égale à la somme des carrés des diagonales.

Dans le cas réel le produit scalaire est défini par

.

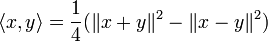
Dans le cas complexe le produit hermitien est défini par

,

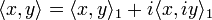
où et i est le nombre complexe 0 + 1i.

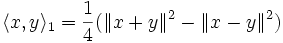
Dans un espace de Hilbert de dimension infinie, le concept habituel de base est remplacé par celui de base de Hilbert qui permet, non plus de décrire un vecteur par ses coordonnées, mais de l'approcher par une suite infinie de vecteurs ayant chacun des coordonnées finies. On est donc au confluent de l'algèbre linéaire et de la topologie. C'est dans le cadre des espaces de Hilbert qu'est développée la théorie de la formulation variationnelle, utilisée dans de nombreux domaines de la physique.

En mécanique quantique, l'état d'un système est représenté par un vecteur dans un espace de Hilbert.

Exemples d'espaces de Hilbert

• muni du produit scalaire usuel.
• L²([a,b]) muni de .
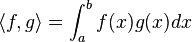
• l², espace des suites de nombres complexes telles que

, le produit scalaire de deux suites u et v étant par définition la somme de la série

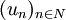
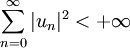
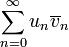
En fait, tout espace de Hilbert séparable est isomorphe à l², voir l'article sur les bases de Hilbert