Base de Hilbert - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une base de Hilbert ou encore base hilbertienne est une généralisation aux espaces de Hilbert de la notion classique de base orthonormée en algèbre linéaire, pour les espaces euclidiens (ou hermitiens dans le cas complexe) de dimension finie.
Comme dans le cas des bases habituelles, il s'agit de pouvoir décomposer n'importe quel vecteur de l'espace en somme de vecteurs colinéaires à ceux de la famille choisie. Cependant dans le cas d'une base de Hilbert, on ne peut pas (généralement) écrire une égalité entre le vecteur décomposé et une combinaison linéaire finie des vecteurs de la base : on doit généralement se contenter d'une série dont les termes sont colinéaires aux vecteurs de la base, et convergeant vers le vecteur à décomposer (la notion de convergence d'une série a ici un sens car un espace de Hilbert est en particulier un espace vectoriel normé).
Remarque : en théorie des hypergraphes, une base de Hilbert est une chose très différente.
Définition
Soit H un espace préhilbertien sur un corps K égal aux nombres réels ou complexes et F une famille (ei) de vecteurs de H où i est élément d'un ensemble I.
Définition — On dit que F est une base de Hilbert de H si et seulement si :
- F est une famille orthonormale de H, c'est-à-dire :
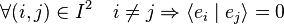
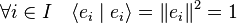
- La famille est de plus complète au sens suivant :
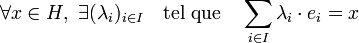
La sommabilité de la famille
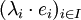
Dans le cas où H est de dimension finie, cette définition coïncide avec celle de base orthonormale. Dans le cas d'un espace de dimension infinie, le terme de base orthonormale indique très généralement une base de Hilbert.
Propriétés
Inégalité de Bessel et coefficients de Fourier
Une première majoration joue un rôle important pour établir les propriétés d'une base de Hilbert. Elle porte le nom d'inégalité de Bessel.
Inégalité de Bessel — Soient E un sous-espace vectoriel fermé de H, (fi) avec i un élément de l'ensemble I une base de Hilbert de E et x un élément de H. Alors la série suivante est absolument convergente et majorée par le carré de la norme de x :
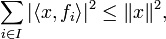
et l'ensemble de ses termes non nuls est au plus dénombrable. L'égalité n'a lieu que si x est élément de E .
Le cas d'égalité est toujours vérifié si E est égal à H, il prend le nom d'égalité de Parseval. C'est une généralisation du théorème de Pythagore, utilisée dans le cadre des séries de Fourier.
La démonstration de l'inégalité de Bessel contient la propriété suivante :
Proposition — Une famille orthonormale de H est une base de Hilbert si et seulement si elle est totale, c'est-à-dire si le sous-espace vectoriel qu'elle engendre est dense dans H.
Ainsi une base de Hilbert de H n'est pas une base au sens algébrique du terme, mais une base orthonormale d'un sous-espace D dont l'adhérence est égale à H.
L'égalité de Parseval permet de déterminer l'expression d'un élément x dans une base hilbertienne (ei) de H :
Théorème et définition — Si (ei) est une base hilbertienne de H, l'égalité suivante est vérifiée :
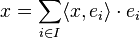
Les coefficients
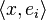
Ainsi, à l'image de la situation pour une base au sens algébrique, il existe une et une unique manière d'exprimer un vecteur dans une base de Hilbert, mais en général comme une série et non plus une somme finie.
Toutes les démonstrations se trouvent dans l'article associé.
Existence
L'existence d'une base hilbertienne n'est pas garantie par les axiomes d'un espace préhilbertien. Il faut ajouter au moins une hypothèse pour la démontrer.
Théorème — Si H est complet ou séparable, alors il existe une base hilbertienne.
-
- Si E est complet, alors il existe une base hilbertienne.
Soit F l'ensemble des parties orthonormales de E, muni de la relation d'ordre inductif l'inclusion. Soit m une famille maximale de F. Son existence est garantie par le lemme de Zorn. Notons H l'adhérence du sous-espace vectoriel engendré par m, et montrons que H=E, ce qui prouvera que m est une base hilbertienne.
Soient x un vecteur de E et y son projeté orthogonal sur H (qui existe, d'après la preuve de l'inégalité de Bessel dans le cas général : il n'est donc pas nécessaire de faire appel au théorème du supplémentaire orthogonal). Alors y-x est orthogonal à H donc nul (par maximalité de m), donc x appartient à H, ce qui permet de conclure que H=E.
-
- Si E est séparable, alors il existe une base hilbertienne.
La logique possède une analogie avec la démonstration précédente, même si le lemme de Zorn n'est plus nécessaire. Soit (fn) une suite dense dans E, il est possible d'en extraire une sous-suite libre (gn)n>0 telle que l'adhérence du sous-espace vectoriel engendré par les gn soit égale à E. Soit (hn)n>0 la suite construite par récurrence de la manière suivante :
Soit n un entier positif ou nul, on suppose déjà construits h1, ... , hn et on note Hn le sous-espace qu'ils engendrent (donc pour n=0 on ne suppose rien, et H0={0}). Soit y le projeté orthogonal de gn+1 sur Hn (qui existe, d'après la preuve de l'inégalité de Bessel dans le cas fini). Alors le vecteur gn+1-y est non nul. En le divisant par sa norme, on construit un vecteur hn+1 de norme 1 orthogonal à Hn (donc à tous les hi précédents) et tel que l'espace vectoriel engendré par Hn et hn+1 contienne gn+1.
La famille (hn) est orthonormale par construction. Les i premiers vecteurs de cette famille engendrent le même espace que les i premiers vecteurs de la famille (gn), les espaces vectoriels engendrés par (hn) et (gn) sont donc confondus, ce qui achève la démonstration.
Un algorithme, dénommé Procédé de Gram-Schmidt, se fonde sur cette logique.

















































