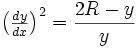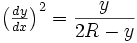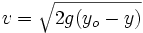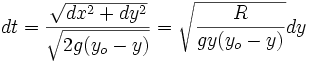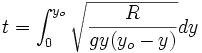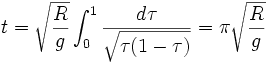Courbe tautochrone - Définition

Une courbe tautochrone est la courbe où le temps pris par une particule glissant sous l'influence uniforme de la gravité jusqu'à son point le plus bas est indépendant de son point de départ.

Le problème tautochrone, l'essai d'identifier cette courbe, fut résolu par Huygens en 1659 dans le cas où seule la gravité agit. Il prouva géométriquement dans son Horologium oscillatorium (Le Pendulum Clock, 1673) que la courbe était une cycloïde. Cette solution fut utilisée ultérieurement pour attaquer le problème de la courbe brachistochrone.

Plus tard, des mathématiciens tels que Lagrange, d'Alembert et Euler cherchèrent une solution analytique au problème dans le cas général.

Démonstration que la cycloïde est une courbe tautochrone

L’équation différentielle décrivant la cycloïde générée par un cercle de rayon R, est:

Pour l’exercice qui nous intéresse on utilise une cycloïde inversée (tête en bas) dont l’équation différentielle prend la forme:

On place une particule sur la courbe à la position de coordonnées (x_o,y_o) et on laisse la gravité agir (constante gravitationnelle g). La vitesse en un point quelconque (x, y) de la courbe est:

Le temps pris par la particule pour effectuer le trajet infinitésimal jusqu’au point de la courbe (x+dx, y+dy) est:

Le temps t que prendra la particule pour arriver au bas de la cycloïde est:

En effectuant le changement de variable on trouve:

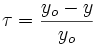
D’où il ressort que le temps de trajet est indépendant du point de départ sur la cycloïde.