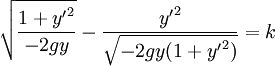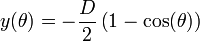Courbe brachistochrone - Définition

Introduction

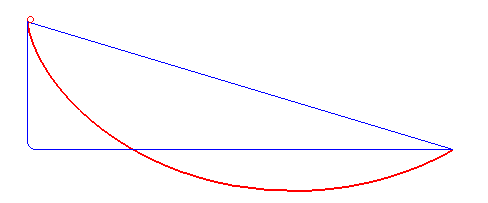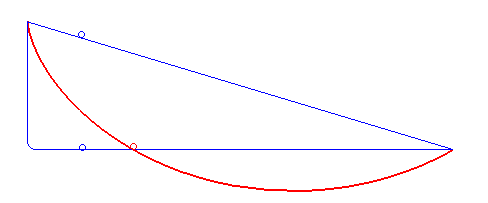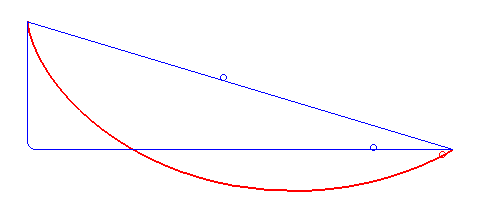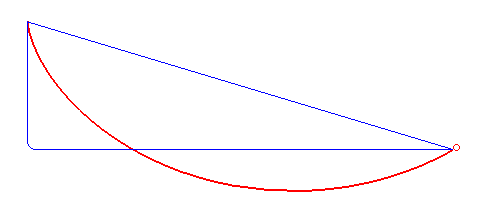
Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes les courbes joignant deux points fixés : on parle de problème de la courbe brachistochrone.

Étymologie

Le mot brachistochrone vient du grec brakhisto (« le plus court ») et s'écrit donc avec un i et non un y, et de chronos (« temps »). Elle fut étudiée et nommée ainsi par Jean Bernoulli.

Démonstration de la solution

Démonstration historique (par Jean Bernoulli)

Le chemin le plus court entre deux points est celui que suivrait un rayon de lumière. La courbe brachistochrone est donc simplement le trajet suivi par la lumière dans un milieu où la vitesse augmente selon une accélération constante (l’attraction terrestre g). La loi de la conservation de l’énergie permet d’exprimer la vitesse d’un corps soumis à l’attraction terrestre par:

,

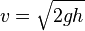
où h représente la perte d’altitude par rapport au point de départ.

La loi de la réfraction, selon le principe de Fermat, indique que tout au long de sa trajectoire un rayon lumineux obéit à la règle

,

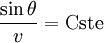
où θ représente l’angle par rapport à la verticale. En insérant dans cette formule l’expression de la vitesse trouvée plus haut, on constate immédiatement deux choses:

1- Au point de départ, lorsque la vitesse est nulle, l’angle doit nécessairement être nul. Donc la courbe brachistochrone est tangente à la verticale à l’origine.

2- La vitesse est bornée car le sinus ne peut être supérieur à 1. Cette vitesse maximum est atteinte quand la particule (ou le rayon) passe par l’horizontale.

Sans restreindre la généralité du problème, on va supposer que la particule part du point de coordonnées (0,0) et que la vitesse maximum est atteinte à l’altitude –D. La loi de la réfraction s’exprime alors par:

.

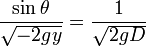
Sachant que la particule se déplace sur une courbe, on a la relation :

.

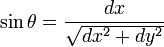
En insérant cette expression dans la formule précédente et en réarrangeant les termes on trouve:

(1 + y'²)y = − D.

Ce qui est l’équation différentielle de l’opposée d’une cycloïde, générée par un cercle de diamètre D.

Démonstration avec le calcul des variations

Soit y = f(x) l'équation cartésienne de la courbe (on exclut les courbes ayant des parties verticales), y étant dirigé vers le haut, et la courbe commençant à l'origine. On exprime un déplacement infinitesimal sur la courbe:

.

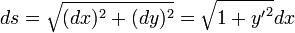
Mais, d'autre part, on a toujours, en vertu du théorème de l'énergie cinétique, la relation suivante :

.

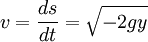
On peut alors exprimer le temps de parcours infinitésimal dt:

.

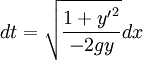
Donc a, avec T le temps de parcours (à minimiser), x_a et x_b les abscisses de départ et d'arrivée.

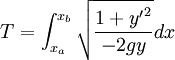
Il s'agit donc de trouver le minimum de la fonctionnelle . Les extrema d'une telle fonctionnelle sont donnés par l'équation d'Euler-Lagrange.

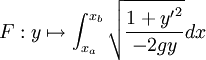
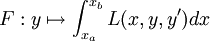
La fonctionnelle ne dépendant pas directement de x, la formule de Beltrami est ici directement applicable, à savoir avec k une constante arbitraire, ce qui donne ici:

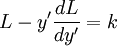
Après multiplication des deux membres par et simplification, on obtient que y est un extrema de F si :

.

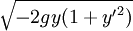
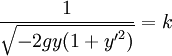
On obtient donc l'équation différentielle (1 + y'²)y = Cste, où la constante n'est autre que -D, altitude minimale atteinte par le point mobile.

Résolution de l'équation différentielle et solution

Pour résoudre (1 + y'²)y = − D, on procède au changement de variable suivant:

.

Dans ce cas, on obtient l'équation paramétrique de la courbe solution:

,

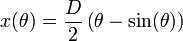
Il s'agit d'une cycloïde renversée, sous sa forme paramétrée :