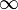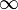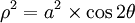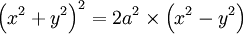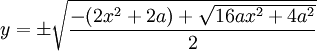Lemniscate de Bernoulli - Définition
La lemniscate de Bernoulli est une courbe plane. Elle porte le nom du mathématicien et physicien suisse Jacques Bernoulli.
Une lemniscate de Bernoulli, de foyers F et F’, est l'ensemble des points M vérifiant la relation :
-
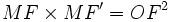
Cette courbe fait partie de la famille des lemniscates, dont elle est l'exemple le plus connu et le plus riche en propriétés. Pour sa définition, elle est l'exemple le plus remarquable d'ovale de Cassini. Elle représente aussi la section d'un tore particulier par un plan tangent intérieurement.
Expressions dans différents systèmes de coordonnées
On pose OF = a. En coordonnées polaires, la lemniscate de Bernoulli admet pour équation :
En coordonnées cartésiennes, on peut la décrire par l'une des deux équations.
- Soit en fonction de x et y :
-
- Soit en fonction de x :
-
Le symbole de l'infini ?
La lemniscate de Bernoulli est souvent considérée comme une courbe qui se parcourt sans fin. Cette caractéristique de la lemniscate serait à l'origine du symbole de l'infini