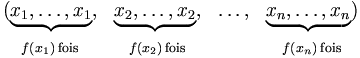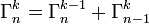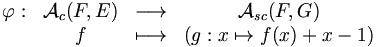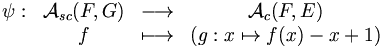Combinaison avec répétition - Définition

Première approche

En mathématiques, lorsque nous choisissons k objets parmi n objets discernables, chaque objet pouvant être répété (au plus k fois), nous obtenons un groupement non ordonné de k objets éventuellement répétés. Mais ce n’est pas acceptable en mathématiques de définir une k-combinaison avec répétition de cette façon, puisqu'un tel groupement n'est pas un ensemble (en effet la définition en extension d'un ensemble empêche la répétition des éléments et par exemple {1, 1, 2, 2, 2, 3}={1, 2, 3})..

Définition :

Une k-combinaison avec répétition d'un ensemble fini E de cardinal n, est une application f de E dans {0, 1, ..., k}, telle que

.

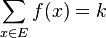
Plus précisément, si E={x₁, x₂, ..., x_n} alors f vérifie

.

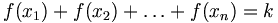
f s'appelle aussi une combinaison de n éléments pris k à k.

Remarque :

Cette application indique pour chaque élément de E le nombre de fois qu'il est choisi; et si l'application associe la valeur 0 à un élément de E, alors l'élément n'est pas choisi. De plus la somme des nombres de répétitions doit bien être égale à k, si nous voulons exactement k objets éventuellement répétés.

Exemple :

Dans un jeu de dominos, un domino est une 2-combinaison avec répétition de l'ensemble E={blanc, 1, 2, 3, 4, 5, 6}. Chaque domino peut être représenté par une application de E dans {0, 1, 2} qui associe à chaque élément de E le nombre de fois où l'élément apparaît sur le domino.
Ainsi le domino blanc, est représenté par l'application f définie par

f(blanc)=2, f(1)=0, f(2)=0, f(3)=0, f(4)=0, f(5)=0 et f(6)=0

et le domino blanc, 1 par l'application f définie par

f(blanc)=1, f(1)=1, f(2)=0, f(3)=0, f(4)=0, f(5)=0 et f(6)=0

Une autre représentation

Soit n un entier naturel non nul, et soit l'ensemble E={x₁, x₂, ..., x_n}. Munissons E d'une relation d'ordre total et supposons que

x₁ < x₂ < ... < x_n

À une k-combinaison avec répétition de E, nous associons le k-uplet croissant (au sens large)

Réciproquement à un k-uplet croissant d'éléments de E (a₁, a₂, ..., a_k), c'est-à-dire un k-uplet tel que

a₁ ? a₂ ? ... ? a_k

nous pouvons associer l'application f:E → {0, 1, ..., k} qui envoie un élément de E sur le nombre de fois où il apparaît dans le k-uplet. Il est alors évident que

f(x₁)+f(x₂)+ ... +f(x_n)=k

et donc que f est une k-combinaison avec répétition de E.

Ainsi, il y a une bijection entre l'ensemble des k-combinaisons avec répétition de E et l'ensemble des k-uplets croissants d'éléments de E, ou encore des applications croissantes (au sens large) de {1, 2, ..., k} dans E.

'Exemple :

Un domino peut être représenté de manière unique par un couple croissant (a, b) tel que a ? b d'éléments de E={blanc, 1, 2, 3, 4, 5, 6}.

Nombre de combinaisons avec répétition

Théorème :

Soit E un ensemble fini de cardinal n ( ). Alors l'ensemble K_k(E) des k-combinaisons avec répétition de E est fini et son cardinal est égal à

,

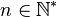
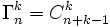
qui est le nombre de k-combinaisons de n+k-1 éléments.

se lit " Gamma nk ".

Démonstration :

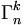
Les combinaisons avec répétition sont des applications d'un ensemble fini dans un autre ensemble fini donc K_k(E) est fini. Supposons que E={x₁, x₂, ..., x_n}. L'ensemble K_k(E) se partitionne en l'ensemble K' des combinaisons qui envoient x₁ sur 0 (représentées par un k-uplet croissant dans lequel x₁ n'apparaît pas) et l'ensemble des combinaisons qui envoient x₁ sur un entier naturel non nul (représentées par un k-uplet croissant dans lequel x₁ apparaît au moins une fois). En restreignant une combinaison de K' à F=E\{x₁} (ce qui revient à la considérer comme un k-uplet croissant d'éléments de F), nous voyons qu'il y a autant d'éléments dans K' que de combinaisons avec répétition de n-1 éléments pris k à k donc . En retranchant 1 à la valeur en x₁ d'une combinaison de (ce qui revient à " éliminer un x₁ " du k-uplet correspondant pour obtenir un (k-1)-uplet), nous transformons cette combinaison en une combinaison avec répétition de n éléments pris k-1 à k-1. Réciproquement, en ajoutant 1 à la valeur en x₁ d'une combinaison de n éléments pris k-1 à k-1, nous obtenons un élément de .
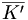
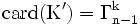
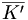
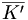
Il y a donc autant d'éléments dans que de combinaisons avec répétition de n éléments pris k-1 à k-1 donc .
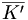
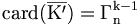
En écrivant

,

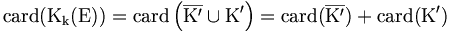
nous obtenons la formule de récurrence

De plus nous avons pour tout entier naturel n non nul, et pour tout entier naturel k et , et nous en déduisons le résultat.

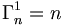
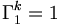
Autre démonstration :

Nous avons vu qu'il y avait une bijection entre l'ensemble des k-combinaisons avec répétition d'un ensemble E et l'ensemble des applications croissantes de F={1, 2, ..., k} dans E. Il suffit donc de déterminer le cardinal de ce dernier ensemble que nous noterons .

Théorème :

Soient n et k deux entiers naturels non nuls, E un ensemble totalement ordonné fini de cardinal n, et F={1, 2, ..., k}. Alors l'ensemble des applications croissantes de F dans E est fini et son cardinal est le nombre de k-combinaisons avec répétition de E, égal à . Et ce cardinal se note .

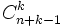
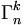
Démonstration :

Sans perte de généralité, nous pouvons supposer que E={1, 2, ..., n}. Nous allons transformer une application croissante de F dans E en une application strictement croissante de F dans une autre ensemble G, en lui ajoutant l'application x ? x – 1.
Posons G={1, 2, ..., n+k-1} et notons l'ensemble des applications strictement croissantes de F dans G. À une application croissante f de F dans E, associons l'application g de F dans G définie par

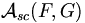
∀ x ∈ F, g(x)=f(x)+x-1

Il est facile de vérifier que l'application

est bien définie. Et l'application

est l'application réciproque de ?.

D'où .

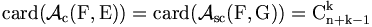
Approche moins "matheuse" des combinaisons avec répétitions

Une combinaison avec répétitions de "k" objets pris parmi "n" objets est une manière de sélectionner "k" objets parmi "n" objets distincts, sans tenir compte de l'ordre des "k" objets et avec répétitions, c’est-à-dire que le même objet peut être sélectionné plusieurs fois.

Le nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets égale :

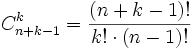
Voici deux démonstrations de cette affirmation.

Première démonstration :
Numérotons les "n" objets de 0 à (n-1).
Remarquez qu'à chaque combinaison avec répétitions de "k" objets parmi les "n", correspond une et une seule permutation avec répétitions de "n-1" boules noires et "k" boules blanches.
Le nombre de boules noires à gauche de la première boule blanche correspond au numéro d'un objet de la combinaison avec répétitions.
Le nombre de boules noires à gauche de la deuxième boule blanche correspond au numéro d'un objet de la combinaison avec répétitions.
etc. pour toutes les boules blanches.
Conclusion :
Le nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets égale le nombre de permutations avec répétitions de "k" boules blanches et de "n-1" boules noires.
Ce nombre vaut :
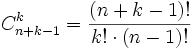
C'est le nombre de permutations des (n+k-1) boules, mais dans lesquelles on ne distingue pas les permutations des boules noires entre elles et des boules blanches entre elles.
On à (n+k-1)! permutations des boules, qu'il faut diviser par les (n-1)! permutations des boules noires et les k! permutations des boules blanches.

Deuxième démonstration :
Numérotons les "n" objets de 0 à (n-1).
Plaçons n boules noires numérotées de 0 à (n-1) et (k-1) boules blanches dans une urne.
Sur la première boule blanche est noté : "remplacez-moi par une boule noire identique à la plus à gauche".
Sur la deuxième boule blanche est noté : "remplacez-moi par une boule noire identique à la deuxième la plus à gauche".
Sur la troisième boule blanche est noté : "remplacez-moi par une boule noire identique à la troisième la plus à gauche".
etc.

On tire de l'urne "k" boules parmi les "n+k-1" boules noires et blanches. On les place par ordre des numéros sur les boules.
Le nombre de résultats possibles de l'expérience précédente est égal au nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets.
Il est également égal au nombre de combinaisons sans répétitions de "k" boules parmi les "n+k-1" boules noires et blanches.

Ce nombre est :

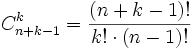
Voyez également

• Combinatoire
• Combinaison