Axiome de l'ensemble des parties - Définition
En mathématiques, l'axiome de l'ensemble des parties est l'un des axiomes de la théorie axiomatique des ensembles, plus précisément des théories des ensembles de Zermelo et de Zermelo-Fraenkel.
L'axiome affirme l'existence pour tout ensemble E, d'un ensemble auquel appartiennent tous les sous-ensembles de E, et seulement ceux-ci. Un tel ensemble est nommé ensemble des parties de E, d'où le nom de l'axiome.
Cet axiome s'écrit dans le langage formel de la théorie des ensembles, qui est un langage égalitaire du premier ordre avec la relation d'appartenance comme seul symbole primitif non logique. On peut tout d'abord définir formellement l'inclusion :
- A ⊂ B signifie ∀ x (x ∈ A ⇒ x ∈ B) .
L'axiome s'écrit alors :
- ∀E ∃P ∀A (A ∈ P ⇔ A ⊂ E).
qui se lit en français :
- Pour tout ensemble E, il existe un ensemble P tel que tout ensemble A est un élément de P si et seulement s’il est une partie de E.
Il n'est pas nécessaire d'énoncer dans l'axiome l'unicité de cet ensemble P pour un E donné. Celle-ci est assurée par l'axiome d'extensionnalité. On peut donc parler de l'ensemble des parties de E, et on note celui-ci habituellement "
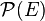
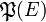
En itérant l'ensemble des parties sur l'ensemble des entiers naturels (voir axiome de l'infini) on arrive vite à des ensembles dont l'utilité en mathématiques n'est pas évidente. Il existe donc des théories faibles des ensembles, comme la théorie des ensembles de Kripke-Platek, qui ne comprennent pas cet axiome. En contre-partie il peut être utile d'ajouter les entiers comme éléments primitifs (ur-elements). L'entier de Von-Neumann n " vit " en effet dans l'ensemble des parties itéré n fois à partir de l'ensemble vide.
Pour prendre un exemple très simple, la logique du second ordre, que l'on peut voir comme une théorie des ensembles très faible, n'a pas d'équivalent de l'axiome de l'ensemble des parties. Mais si on a les entiers (donnés par exemple par 0 et un symbole pour le successeur) dans le langage, on peut développer l'arithmétique du second ordre, et donc, avec quelques axiomes, une théorie suffisante pour l'analyse réelle usuelle (on a les entiers et les ensembles d'entiers, mais pas les ensembles d'ensemble d'entiers).
En théorie des types, les sous-ensembles d'un ensemble E sont d'un type différent, plus complexe, que les élements de E.

















































