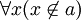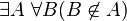Axiome de l'ensemble vide - Définition

L'axiome de l'ensemble vide est, en mathématiques l'un des axiomes possibles de la théorie axiomatique des ensembles. Comme son nom l'indique, il permet de poser l'existence d'un ensemble vide. Dans les présentations modernes, il n'est plus mentionné parmi les axiomes des théories des ensembles de Zermelo, ou Zermelo-Fraenkel, car il est conséquence en logique du premier ordre du schéma d'axiomes de compréhension.

Exposition

Dans le langage formel des axiomes de Zermelo-Frankel, l'axiome s'écrit :

ou en d'autres termes :

Il existe un ensemble A tel que, pour tout ensemble B, B n'est pas un élément de A, c’est-à-dire qu'il existe un ensemble dont aucun ensemble n'est élément.

L'axiome d'extensionnalité peut être utilisé pour démontrer que cet ensemble est unique. Il est appelé l'ensemble vide et il est noté ou {}.

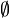
Essentiellement, l'axiome affirme donc que l'ensemble vide existe.

Ensemble vide et schéma de compréhension

L'existence de l'ensemble vide peut être démontrée par compréhension, et donc n'a pas à faire partie des axiomes de la théorie des ensembles de Zermelo ou de Zermelo-Fraenkel, quand celles-ci sont vues comme des théories du premier ordre. En effet, en logique du premier ordre, les domaines d'interprétation des variables d'objets de base, ici des variables d'ensemble, sont non vides. Cela compliquerait beaucoup l'exposé des règles logiques de considérer des domaines vides. C'est ce qui permet l'introduction de nouvelles variables dans le raisonnement : dès que l'on introduit une nouvelle variable, on suppose qu'elle désigne un objet.

Il suffit donc, dans le cas qui nous préoccupe, d'appliquer le schéma d'axiomes de compréhension à un ensemble arbitraire, pour une propriété jamais réalisée : soit y un ensemble, a={x ∈ y| x ≠ x} est bien l'ensemble vide, c’est-à-dire que .