Constante de Brun - Définition
En mathématiques, la constante de Brun des nombres premiers jumeaux (ou plus simplement constante de Brun) est la somme de la série des inverses des nombres premiers jumeaux, c’est-à-dire des couples de nombres premiers distants de 2.
Cette constante tire son nom du mathématicien Viggo Brun qui démontra en 1919 que cette série est convergente[1].
Définition
Soit
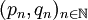
Soit
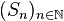
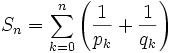
-
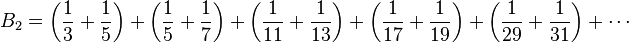
À la différence de la série des inverses de tous les nombres premiers qui, elle, diverge, cette série est convergente. Une divergence de la série aurait permis de prouver la conjecture des nombres premiers jumeaux ; dans la mesure où elle est convergente, cette conjecture n'est toujours pas prouvée.
Estimation
Une première estimation de la constante de Brun a été effectuée par Shanks et Wrench en 1974 à l'aide des premiers jumeaux jusqu'à 2 millions[2]. R.P. Brent calcula en 1976 tous les nombres premiers jumeaux jusqu'à 1011 et améliora le résultat[3].
Une meilleure estimation de la constante de Brun a été réalisée par Thomas Nicely en 1994 par une méthode heuristique en calculant les nombres premiers jumeaux jusqu'à 1014[4] (pour l'anecdote, T. Nicely a mis en évidence à cette occasion le bogue de la division du Pentium). Il a par la suite amélioré cette approximation en utilisant les jumeaux jusqu'à 1,6×1015 (lien) et a mis à jour cette approximation au fil des années. En septembre 2006, il donnait l'estimation suivante (lien) :
- B2 = 1,90216 05825 38 ± 0.00000 00014 00.
La meilleure estimation de l'écriture décimale de la constante de Brun a été réalisée en 2002 par Pascal Sebah et Patrick Demichel en utilisant tous les nombres premiers jumeaux jusqu'à 1016[5] :
- B2 ≈ 1,90216 05831 04.
La suite des chiffres de la constante de Brun en écriture décimale est référencée dans l'OEIS comme la séquence la séquence A065421 de l'OEIS.
Généralisation
Il existe aussi une constante de Brun pour les quadruplets de nombres premiers. Un quadruplet de premiers est un couple constitué de jumeaux premiers, séparés d'une distance de 4 (la plus courte distance possible) soit (p,p + 2,p + 6,p + 8). Les premiers quadruplets de premiers sont (5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109). La constante de Brun pour les quadruplets de premiers, notée B4, est la somme des inverses de tous les nombres premiers des quadruplets:
avec la valeur:
- B4 = 0,87058 83800 ± 0,00000 00005.