Logique d'ordre supérieur - Définition

Les logiques d'ordre supérieur sont des logiques formelles qui étendent le calcul des prédicats du premier ordre en permettant d'utiliser les variables dans les termes en tant que fonctions, et dans les expressions en tant que prédicats.

D'un point de vue sémantique, cela revient à dire que l'on considère les fonctions et prédicats comme des objets à part entière, au même titre que, par exemple, un nombre entier. On s'autorisera ainsi, d'une part, à quantifier les prédicats et fonctions et, d'autre part, à donner des fonctions ou des prédicats en arguments d'autres fonctions et prédicats. Néanmoins, on pourra se doter d'un système de typage qui restreindra le genre d'objet qui pourra être donné en tant que tel ou tel argument de tel ou tel prédicat ou telle ou telle fonction.

Un prédicat d'ordre supérieur est un prédicat qui prend comme argument un ou plusieurs autres prédicats. De manière générale, un prédicat d'ordre n prend comme argument un ou plusieurs prédicats d'ordre n-1, avec n > 1. La même chose est valable pour les fonctions d'ordre supérieur.

Les lambda-calculs typés, comme le calcul des constructions, s'inspirent de telles logiques dans ce qu'on appelle le paradigme fonctionnel. Un lien fort est tissé entre les mathématiques et l'informatique grâce à l'isomorphisme de Curry-Howard qui associe un lambda-calcul à une logique. C'est de ce domaine que sont issus les langages de programmation fonctionnelle.

Logique du second ordre

La logique du second ordre étend celle du premier ordre par l'ajout de variables fonctionnelles, qui peuvent donc être quantifiées. Par exemple, .

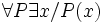
La logique monadique du second ordre se restreint aux variables fonctionnelles unaires, qui sont en fait les ensembles. Elle permet d'avoir des résultats de décidabilité plus intéressants qu'au premier ordre : par exemple, la théorie monadique d'un ordinal dénombrable est décidable.

Logique du troisième ordre

Elle utilise des objets de troisième type, comme les filtres ou ultrafiltres, mais est rarement mentionnée en tant que telle.