Courbe de taux - Définition
En finance, l'expression courbe de taux désigne la représentation graphique ou mathématique en fonction de leur durée des taux d'intérêt, constatés à un moment donné sur un marché financier, d'une même classe d'instruments fongibles exprimés dans une même devise, comme les swaps contre IBOR.
Par extension, on l'emploie pour des instruments non fongibles mais néanmoins fortement comparables entre eux, comme les emprunts à taux fixe d'un même État.
Les taux représentés sont généralement soit des taux actuariels, soit, ce qui est plus rigoureux, des taux zéro-coupon.
En anglais, on emploie indifféremment les expressions yield curve, "courbe de rendement", ou term structure of interest rates, "structure à terme des taux d'intérêt".
Les marchés de taux d'intérêt
Aux États-Unis et dans la zone euro, ainsi que, dans une moindre mesure, au Japon et en Grande Bretagne, il existe en permanence deux marchés de référence des taux d'intérêt de 0 à 30, voire 50 ans, d'une très grande liquidité :
- celui des principaux emprunts d'État à taux fixe;
- celui des swaps contre IBOR.
Pour les taux d'intérêt des autres devises, cela est un peu moins vrai car toutes les échéances d'emprunts d'État n'existent pas nécessairement ou ne sont pas forcément liquides.
Seul le marché des swaps permet, stricto sensu, de tracer une véritable courbe des taux. En effet, à la différence de valeurs mobilières, ils n'ont pas d'existence physique, et donc :
- ils sont entièrement fongibles et réductibles à leurs coefficients d'actualisation ;
- et de plus, leur encours est quasi-illimité : il ne peut véritablement y avoir de corner sur les swaps, et leurs prix de marchés peuvent donc être beaucoup plus cohérents mathématiquement et beaucoup moins dépendants de l'offre et de la demande instantanée que les prix des obligations, même ceux des plus liquides d'entre elles, les emprunts d'État.
Par ailleurs, les swaps fournissent une courbe au pair, c'est-à-dire où le taux actuariel est égal au taux nominal, donc sans les distortions dues à un taux nominal hors marché (voir : taux zéro-coupon).
Néanmoins, le marché directeur des taux à moyen et long terme reste celui des emprunts d'État :
- via les futures sur Bunds d'Eurex dans la zone euro ;
- via les futures sur T-Note du Chicago Board of Trade aux États-Unis.
À défaut d'être parfaitement cohérentes mathématiquement, les courbes d'emprunts d'État fournissent à l'économie des taux sans risque et donc un point d'ancrage global pour toutes les mesures de rentabilité. Historiquement, ce sont les premières à avoir été tracées, aux États-Unis dans les années 1970 et plus précisément, suivant la tradition, chez Salomon Brothers, alors que les swaps et autres dérivés de taux d'intérêt n'existaient pas encore, hormis des forwards.
Propriétés des courbes de taux
Taux forward implicites
Toute courbe de taux d'intérêt spot (c'est-à-dire pour départ immédiat) contient en elle-même des prévisions de taux pour l'avenir. D'une façon plus générale, à partir du moment où on dispose :
- du taux d'un instrument pour A années
- et de celui d'un instrument fongible pour B années, avec B>A,
on dispose également de celui, implicite, pour la durée C=B-A années commençant dans A ans, appelé taux C ans forward dans A ans et noté AxB. Par exemple, 1x4 désignera le taux à 3 ans dans un an et 2x5 celui à 3 ans dans deux ans.
Plus généralement, si on dispose de la courbe des taux de 0 à B ans, on dispose aussi de toutes les courbes de taux de 0 à C ans dans A années, pour tout A Ainsi, de la courbe 0-30 ans on peut déduire aussi bien : etc. Malheureusement, plus on avance dans l'avenir, et plus des variations faibles de la pente de la courbe des taux ont des conséquences importantes pour les taux forward. Pour employer une expression imagée, le poids du futur antérieur va croissant... Par exemple, si le taux zéro-coupon d'un instrument à 10 ans est 5%, et celui du même instrument à 11 ans est 5.5%, alors le taux implicite du 1 an dans 10 ans est : Une variation faible (50 points de base) spot a un effet de plus de 500 points de base dans 10 ans. Ce qu'il est important de retenir, c'est qu'une courbe des taux croissante contient la prévision d'une courbe des taux plus haute dans l'avenir. Cela est illustré par le graphe 1 : en rouge est représentée une courbe spot 0-30 ans, en bleu celle 0-29 ans implicite un an après. La cohérence des courbe des taux se mesure à celle des taux courts forwards implicites qui en découlent. Les graphes 2 et 3 illustrent bien cela. Le graphe 3 représente en rouge la même courbe des swaps en euros que le graphe 1, mais en bleu figure celle des 1 an forwards au cours des 29 prochaines années. De même, le graphe 2 représente en rouge la courbe des taux des emprunts d'État français de 0 à 50 ans et en bleu les taux forwards 1 an pendant les 49 prochaines années. Autant les forwards de swaps sont cohérents, autant ceux des emprunts État sont soumis à de fortes variations peu cohérentes. Pourtant la courbe spot des emprunts d'État, en rouge, ne donne pas à première vue l'impression d'être irrégulière ou bosselée. D'une façon générale, les courbes de taux sont concaves et croissantes, au moins sur leur partie 0-10 ans. Pour être plus précis, les taux à 3 mois d'un type d'instrument donné sont le plus souvent plus bas (et, dans des cas exceptionnels, plus haut) que ceux à 10 ans du même type d'instrument. Cette structure vient, selon l'explication traditionnelle (voir : Aversion au risque), d'une préférence naturelle des investisseurs pour la liquidité et donc pour les instruments de taux à court terme. Contre une immobilisation plus longue de leur épargne, et une volatilité accrue des mouvements de prix de celle-ci, ils exigeraient une rémunération supplémentaire. Une courbe de taux inversée, c’est-à-dire descendante sur sa partie 0-10 ans, ce qui est assez rare, indique que l'argent à court terme est plus cher que l'argent à long terme. C'est le cas : Le graphe 4 montre une situation de ce type. La courbe spot, en rouge, est inversée parce qu'en fait : On a vu plus haut que plus on avançait dans le futur et plus l'impact de variations faibles des taux spot avaient une importance grandissante sur les taux forwards implicites. En conséquence, les courbes de taux sont assez plates sur leur partie 10-50 ans, voire légèrement décroissantes. Cela est dû à une convexité supérieure des instruments les plus longs. Il y aurait, si la courbe 10-50 ans était fortement positive, un arbitrage sans risque à acheter du 50 ans et à vendre du plus court, comme du 15 ans, ce qui constitue une position à "gamma positif", et à ajuster en permanence le ratio de couverture au cours du temps, engrangeant marginalement l'effet de nombreux petits mouvements de marché. La comparaison de courbes de taux à deux dates différentes permet de se rendre compte de quelle façon les taux ont évolué. Par exemple si les taux à court terme ont monté plus ou moins que les taux à long terme. La situation et l'évolution des courbes des taux sont considérées comme un signal de ce que sont les anticipations du marché (fournisseurs et utilisateurs de capitaux empruntés) concernant la croissance économique et l'inflation. Une courbe fortement croissante, en particulier, anticipe une croissance économique forte ou une inflation importante, voire les deux.
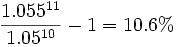
Cohérence des courbes de taux
Formes de courbes - partie 0-10 ans
Formes de courbes - partie 10-50 ans
Importance économique des comparaisons de courbes de taux

















































