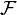Théorème de Radon - Définition
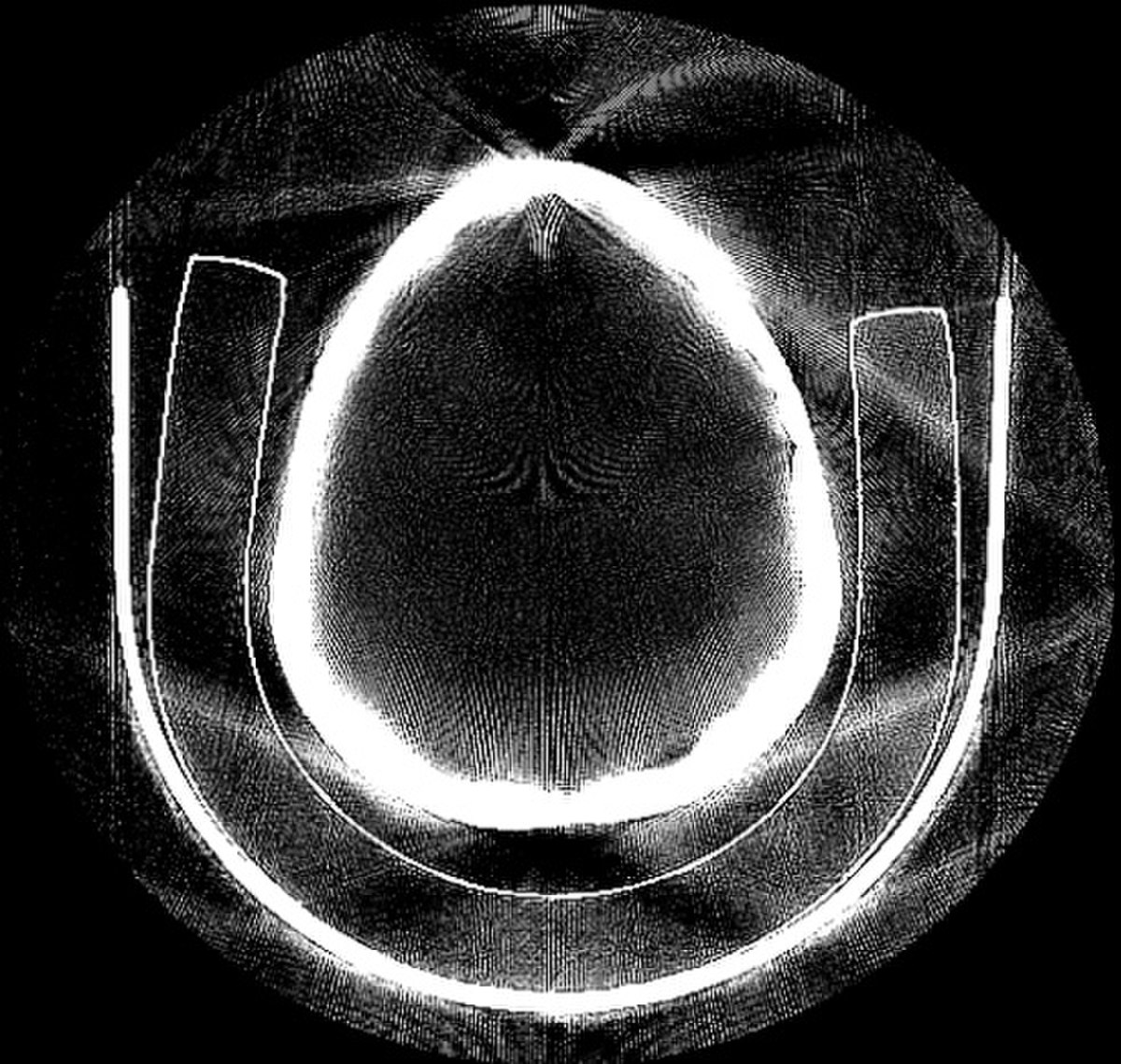
Le théorème de Radon établit la possibilité de reconstituer en volume un objet au moyen de la totalité de ses projections. Ce théorème offrait la théorie permettant de réaliser des appareils de tomodensitographie alias scanners médicaux. Il doit son nom au mathématicien Johann Radon
En toute rigueur, il est bien entendu impossible de disposer de toutes les projections d'un objet solide, mais compte-tenu des corrélations connues (voir morphologie mathématique), on sait majorer l'erreur obtenue en ne prenant par exemple qu'une projection par degré angulaire. Les méthodes d'entropie maximale (voir théorème de Cox-Jaynes) permettent de suppléer à l'information manquante en restant en dessous du seuil de bruit acceptable.
Transformée de Radon
La transformée de Radon est la formulation mathématique d'une projection. La transformée de Radon d'une fonction bidimensionnelle f est donné par l'intégrale selon une direction

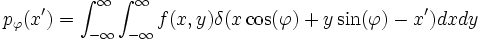
Où δ(x) est l'impulsion de Dirac.
Dans le cas où x' et

Transformée inverse de Radon
La reconstruction de la fonction f en coordonnées polaires peut alors être réalisée à l'aide de la transformée inverse de Radon:
![\hat{f}(r,\theta)=\int_{-\infty}^{\infty} \mathcal{F}^{-1}[|\omega |]*p_{\varphi}(x')d\varphi](https://static.techno-science.net/illustration/Definitions/autres/7/7ec46e5d26841b6306b52ffde373fce8_6bc4ae8f39c5df0a746ec4f9f0f1b0ed.png)
Où