Ensemble stable de poids maximal - Définition
Définition du problème
Dans un graphe non orienté sans boucle ni arête multiple (cf. définitions dans théorie des graphes), noté G = (X, V), on recherche un ensemble stable de poids maximal (noté ESPM).
Un ensemble S inclus dans X est dit stable si et seulement si deux sommets distincts de S ne sont pas adjacents, c’est-à-dire, Γ(G) étant l'ensemble des sommets adjacents aux éléments de S, si et seulement si Γ(G) ∩ S = ∅.
- Un ensemble stable de G est maximal si et seulement s'il n'est contenu dans aucun autre ensemble stable de G.
- On associe à chaque sommet x de X un poids positif ou nul noté p(x) et on définit alors le poids P(S) d'un ensemble stable S par :
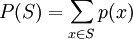
Le problème de l'ESPM consiste à déterminer dans G un ensemble stable S0 tel que
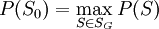
On notera qu'il existe un problème voisin qui est celui de l'ensemble stable de cardinal maximal (ESCM), qui se définit par :
- Soit SG la famille des ensembles stables de G, le nombre de stabilité est : .
- Le problème de l'ESCM consiste à déterminer dans G un ensemble stable de cardinal α(G). Il s'agit d'un cas particulier d'ESPM où les poids sont égaux à 1.
- Le problème de l'ESPM, tout comme celui de l'ESCM, est NP-complet au sens de la théorie de la complexité.
Problèmes directement équivalents
- Une clique de G est un ensemble de sommets
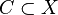
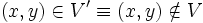
- Un support de G est un ensemble de sommets
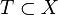
- Un ESPM de G est une clique de poids maximal de G', T est un support de poids minimal si et seulement si X − T est un ESPM.
Autres problèmes équivalents
La recherche d'un ESPM dans un graphe permet la résolution des problèmes de maximisation de fonction pseudo-booléennes et de partitionnement.
- Étant donné une fonction pseudo booléenne f, on va construire un graphe en associant à chaque monôme un sommet du graphe en construction, de poids valant le coefficient dudit monôme. Une arête est générée entre deux sommets lorsque le produit booléen des monômes est nul. Ainsi le maximum de la fonction est égal au poids de l'ESPM du graphe.
- Exemple :
-
- Soit
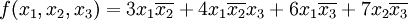
- Le graphe généré est le suivant :
- Soit
-
- L'ESPM (3,4) a pour poids 13, le maximum de la fonction vaut 13.
- Problème de partitionnement.
- Exemple :
- Chercher le minimum de 2x1 + 3x2 + 7x3 + 4x4 + 8x5 avec les contraintes :
- x4 + x5 = 1
- x2 + x3 + x4 = 1
- x3 + x4 = 1
- x1 + x2 + x4 = 1
- Le graphe généré est le suivant :
- Chercher le minimum de 2x1 + 3x2 + 7x3 + 4x4 + 8x5 avec les contraintes :
-
- L'ESPM trouvé est (1, 3, 5).
- La solution est
- x1 = 1
- x2 = 0
- x3 = 1
- x4 = 0
- x5 = 0

















































