Problème à N corps - Définition
Le problème à N corps consiste à résoudre les équations du mouvement de Newton de N corps interagissant gravitationnellement, connaissant leurs masses ainsi que leurs positions et vitesses initiales.
Il s'agit d'un problème mathématique fondamental pour l'astronomie classique, c’est-à-dire dans le cas où les effets de la théorie de la relativité générale d'Einstein peuvent être négligés : vitesses des corps petites devant la vitesse de la lumière dans le vide, et champs de gravitation faibles, ce qui est essentiellement le cas dans notre système solaire.
Le problème à N corps se pose également dans le cadre de la relativité générale ; son étude y est encore plus difficile que dans le cadre newtonien.
Formulation mathématique
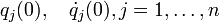
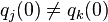
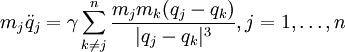
Problème à deux corps
Premier triomphe de la mécanique de Newton, le problème à deux corps, est entièrement soluble analytiquement mouvement keplerien: on dit qu'il s'agit d'un problème intégrable. Tous les étudiants de premier cycle en physique en découvrent un jour les rouages. [1]
Problème à N corps
En dehors de quelques cas rarissimes où une solution exacte est connue, il faut en général recourir à des méthodes de résolutions approchées. Deux approches sont utilisées :
- la théorie des perturbations, qui permet de faire des calculs analytiques approchés sous la forme de développements en série.
- l'analyse numérique. En programmation, le problème de la simulation de N corps devrait être théoriquement d'ordre N2, car toutes les interactions de corps deux à deux devraient être considérées a priori. Des considérations de découpage spatial récursif (Voir: Algorithme de Barnes-Hut) permettent cependant d'arriver à de très correctes approximations en un temps de l'ordre de NlogN seulement.
Remarque sur le problème à trois corps
Contrairement à une idée répandue, le problème à trois corps possède une solution analytique exacte, découverte par Sundman en 1909 [HE01]. Malheureusement, cette solution se présente sous la forme d'une série infinie qui converge très lentement, ce qui la rend inutile en pratique pour faire des prédictions en un temps raisonnable.

















































