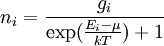Statistique de Fermi-Dirac - Définition

Articles de physique quantique |
| Théorie quantique |
| Électrodynamique quantique |
| Mécanique quantique |
| Théorie des champs |
| Modèle standard |
| Statistiques quantique |
| Bose-Einstein |
| Fermi-Dirac |
| Maxwell-Boltzmann |
| Physiciens |
| Bohr - de Broglie |
| Bose - Einstein |
| Fermi - Dirac |
| Heisenberg - Pauli |
| Schrödinger - Feynman |
En mécanique quantique, la statistique de Fermi-Dirac désigne la distribution statistique de fermions indiscernables (tous similaires) sur les états d'énergie d'un système à l'équilibre thermodynamique. La distribution en question tient à une particularité des fermions : les particules de spin demi-entier sont assujetties au principe d'exclusion de Pauli, à savoir que deux particules ne peuvent occuper simultanément un même état quantique.
Statistique de Fermi-Dirac
La statistique de Fermi-Dirac a été introduite en 1926 par Enrico Fermi et Paul Dirac. En 1927 elle fut appliquée aux électrons dans un métal par Arnold Sommerfeld. Statistiquement, le nombre ni de particules dans l'état d'énergie Ei est donné par
où :
- gi est la dégénérescence de l'état d'énergie Ei , à savoir le nombre d'états possédant cette énergie ;
- μ est le potentiel chimique ;
- k est la constante de Boltzmann ;
- T est la température absolue.
Limite classique et comparaison avec les bosons
À haute température, lorsque les effets quantiques ne se font plus sentir, la statistique de Fermi-Dirac tend vers la statistique de Maxwell-Boltzmann; il en est de même pour la statistique de Bose-Einstein qui régit les bosons. À basse température, si les particules occupent en priorité les niveaux d'énergie les plus faibles, les statistiques diffèrent cependant. Par exemple, à température nulle :
- avec la statistique de Fermi-Dirac, le niveau de plus basse énergie, E0 , est occupé par au plus g0 fermions; les états de basse énergie Ei sont ensuite occupés chacun dans l'ordre croissant des énergies par au plus gi fermions jusqu'à épuisement de ces derniers;
- avec la statistique de Bose-Einstein, le niveau de plus basse énergie contient tous les bosons (cas limite du condensat de Bose-Einstein).
Gaz de fermions quantiques
Les électrons dans les solides forment un gaz de fermions dont la description requiert la statistique de Fermi-Dirac. Récemment, le refroidissement de gaz d'atomes dilués fermioniques jusqu'à des températures de l'ordre du μK a permi d'obtenir des gaz de fermions dégénérés, uniquement descriptibles par cette statistique