Onde de Bloch - Définition
Dans le cadre du cristal parfait infini, les électrons sont soumis à un potentiel périodique ayant la symétrie de translation des atomes constituant le cristal. Les ondes de Bloch (d'après Felix Bloch) sont des fonctions d'ondes décrivant des états quantiques électroniques ayant la même symétrie que le cristal.
Le théorème de Bloch
On considère un cristal parfait infini. Les potentiels possèdent donc la périodicité du réseau cristallin. Examinons les états propres d'énergie d'un électron dans ce réseau.
Si nous baptisons par
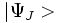
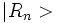
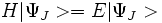
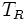
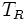
En utilisant la propriétés d'invariance de la norme des états propres par translation d'une période entière du réseau cristallin et la propriété de combinaison des translations, on obtient les valeurs propres de
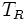
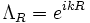
On en déduit que la forme générale de la fonction d'onde dans le cas d'un cristal est
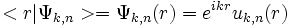
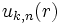
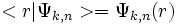
Conséquences du théorème de Bloch
Le théorème de Bloch introduit un vecteur d'onde k. Il est nommé pseudo-moment de l'électron. Cette quantité remplace le moment
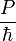
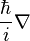
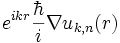
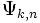
Les zones de Brillouin
En se plaçant dans l'espace réciproque, c'est-à-dire l'espace des k, on vérifie qu'on peut décrire l'énergie d'un état de Bloch en fonction de son vecteur k. On remarque tout de suite que k est défini à un vecteur du réseau réciproque près, à cause de la périodicité du facteur
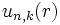
Les bandes interdites
Apparition des bandes interdites
La tradition pédagogique des cours de physique des solides est de faire apparaître la structure des bandes interdites par l'application d'un potentiel cristallin perturbatif (donc arbitrairement faible) sur des électrons libres: c'est le modèle des électrons presque libres. Partons d'une fonction d'onde d'électron libre
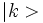
prenons le potentiel cristallin sous la forme:
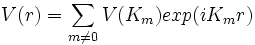
Constatons d'abord que la perturbation introduite par ce potentiel ne peux pas être dans le cas général général une perturbation du premier ordre. En effet, tous les termes de ce potentiel sont oscillatoires et leur moyenne par toute fonction d'onde K sur un domaine suffisamment grand est nulle, sauf si les termes oscillatoires se compensent. On montre facilement que la fonction d'onde prend la forme:
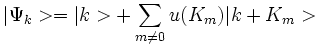
avec:
![u(K_m)={{2m.V(K_m)}\over{{\hbar^2}[E(k)-(k+K_m)^2]}}~](https://static.techno-science.net/illustration/Definitions/autres/c/cf15af74d39212ef1bd99682e8d7b025_fb3165216fbe9a88a2aee723892514a0.png)
Remarquons au passage que cette fonction d'onde est bien une onde de Bloch (il suffit de remplacer les kets par leurs formes fonctionnelles). En posant E(k) = k2 et vu la nature périodique du potentiel perturbateur V, toutes ces contributions sont nulles à l'exception de celles remplissant les conditions de Bragg, c.a.d.
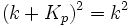
![E={{\hbar^2k^2}\over{2m}}\pm[V(K_p)]~](https://static.techno-science.net/illustration/Definitions/autres/0/0b438c7f6ea4ec16b35e385fa07d2336_7e9491e2800ed2203e501995a9509563.png)
Donc pour un point k à mi distance de l'origine et d'un premier nœud du réseau réciproque, c’est-à-dire
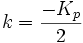
Forme des fonctions d'onde au voisinage de la frontière de zone
Au voisinage de points
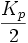
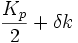
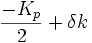
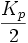
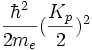
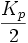
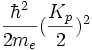
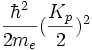
Bibliographie
- Charles Kittel, Solid State Physics, Wiley (1995). ISBN 0471111813
- Ashcroft et Mermin, Physique des solides, Brooks Cole (2003, version française du livre paru en 1976). ISBN 2868835775
- O. Madelung, Introduction to Solid State Physics, Springer, 1981. ISBN 0-387-08516-5
- Blokhintsev, Mécanique quantique et applications à l'étude de la structure de la matière, Dunod, 1967. ISBN 2225509204
- Blokhintsev, Physique du solide

















































