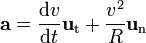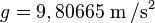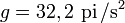Accélération - Définition

Accélération en mécanique

En dynamique, l'accélération subie par un corps est liée à la force totale exercée sur celui-ci par l'intermédiaire de la seconde loi de Newton (ou principe fondamental de la dynamique) selon laquelle

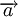
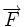
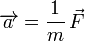
où m est la masse du corps.
Cette équation signifie que toute force appliquée à un objet produit automatiquement une accélération, quelle que soit la masse de cet objet.

L'accélération d'un point peut donc se calculer par la seconde loi de Newton, mais il existe une autre méthode pour la calculer, lorsque l'équation horaire du mouvement est donnée ou calculable facilement : il s'agit de primitiver cette équation horaire du mouvement une première fois (ce qui nous donnera la valeur de la vitesse en fonction du temps), puis une deuxième fois, ce qui donnera la valeur de l'accélération en fonction du temps.

Accélération moyenne

L'accélération moyenne a sur un intervalle de temps Δt est définie de la manière suivante :

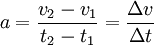
v est la vitesse (vectorielle) à l'instant t et v est la vitesse à l'instant t.

v - v est un vecteur. Il est parfois commode de distinguer l'accélération tangentielle (dans le sens du mouvement, selon le vecteur  : variation de vitesse absolue) et l'accélération normale ou centripète (perpendiculaire au mouvement, selon le vecteur  : à vitesse absolue constante) :

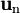
Accélération et gravité

La gravité provoque l'accélération d'une masse qui n'est soumise qu'à cette seule force, lors du mouvement qui par définition est appelé la chute libre. L'intensité de la gravité subie par un corps est donc exprimée sous la forme d'une accélération, notée . Afin de donner une valeur « parlante », on exprime souvent une accélération par rapport à l'accélération moyenne de la gravité sur Terre, en g :

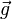
À partir du constat que masse grave et masse inerte ne peuvent être distinguées fonctionnellement, la relativité générale admet, sous le nom de principe d'équivalence, que la gravité ne se distingue pas localement (c'est-à-dire si l'on considère uniquement un point) d'une accélération. Il est important sur le plan conceptuel de connaître cette équivalence, beaucoup de physiciens utilisant pour cette raison, en abrégé, le terme accélération pour désigner indifféremment une modification de vitesse ou la présence dans un champ de gravité, même en l'absence apparente (dans l'espace 3D) de mouvement.

Variations d'accélération

Tout comme le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps on peut définir la dérivée de l'accélération par rapport au temps. Il s'agit du vecteur jerk qui permet ainsi de quantifier les variations d'accélération et qui est utilisé dans un certain nombre de domaines.