Algorithme de tracé de segment de Bresenham - Définition

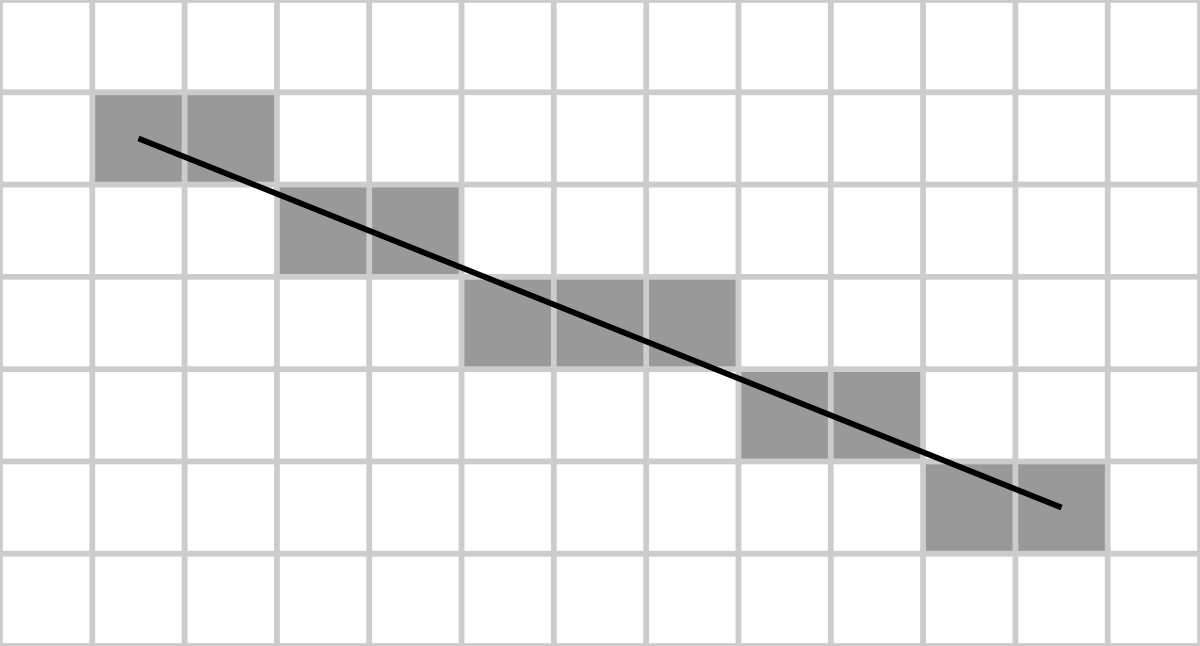
Explication de l’algorithme de base dans le premier octant

Illustration du résultat de l’algorithme de tracé de segment de Bresenham.

La ligne est tracée entre deux points (x₁, y₁) et (x₂, y₂), où chaque paire indique la colonne et la rangée, respectivement, croissant vers le bas et la droite. Nous supposerons au départ que notre segment descend vers le bas et la droite, et que la distance horizontale x₂-x₁ excède la distance verticale y₂-y₁ (c’est-à-dire que le segment a une pente inférieure ou égale à 1). Notre but est, pour chaque colonne x entre x₀ et x₁, d’identifier la rangée y dans cette colonne qui est la plus proche du segment idéal et de tracer un pixel en (x, y).

Détermination des ordonnées

Maintenant, comment pouvons-nous déterminer quel pixel est le plus proche de la droite pour une colonne donnée ? La formule générale d’une droite entre les deux points est donnée par :

.   (1)

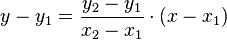
Puisque nous connaissons la colonne , la rangée du pixel le plus proche de l’ordonnée exacte du point d’abscisse sur la droite est donnée en arrondissant cette ordonnée à l’entier le plus proche :

.   (2)

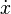
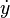
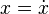
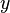
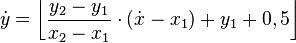
Cependant, le calcul explicite de cette valeur pour chaque colonne est coûteux. Or commence en , et que chaque fois que nous ajoutons 1 à l'abscisse, nous ajoutons la valeur constante à la valeur de l’ordonnée du point de la droite correspondant. Cette valeur est la pente de la droite, et en vertu de notre hypothèse initiale, elle est comprise entre 0 et 1. Après l’arrondi, pour chaque colonne , nous utilisons donc soit la valeur précédente (ordonnée du pixel d'abscisse ), soit cette valeur augmentée de 1.

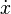
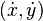
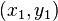
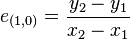
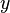
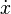
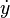
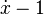
On peut décider laquelle de ces deux valeurs prendre en conservant une valeur d’erreur qui représente la distance verticale entre la valeur courante et la valeur y exacte pour la droite à l’abscisse courante. Au départ cette valeur d’erreur e est nulle et chaque fois que nous incrémentons , nous augmentons la valeur d’erreur par la valeur de pente ci-dessus. Chaque fois que l’erreur dépasse 0,5, la droite est devenue plus proche de la valeur suivante, aussi nous ajouterons 1 à en retranchant simultanément 1,0 à l’erreur e.

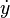
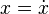
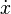
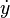
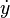
La procédure ressemble à ceci, en supposant que tracerPixel(x, y) est une primitive graphique traçant le pixel de rangée x et de colonne y ; exprimé en pseudo-code, l’algorithme de base est :

      procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est        déclarer entier x, y, dx, dy ;        déclarer rationnel e, e(1,0), e(0,1) ;  // valeur d’erreur et incréments        dy ← y2 - y1 ;        dx ← x2 - x1 ;        y ← y1 ;  // rangée initiale        e ← 0,0 ;  // valeur d’erreur initiale        e(1,0) ← dy / dx ;        e(0,1) ← -1.0 ;        pour x variant de x1 jusqu’à x2 par incrément de 1 faire          tracerPixel(x, y) ;          si (e ←  e + e(1,0)) ≥ 0,5 alors  // erreur pour le pixel suivant de même rangée            y ←  y + 1 ;  // choisir plutôt le pixel suivant dans la rangée supérieure            e ←  e + e(0,1) ;  // ajuste l’erreur commise dans cette nouvelle rangée          fin si ;        fin pour ;      fin procédure ;      

Amélioration de l’algorithme pour le calcul avec des entiers

Le problème avec cet algorithme simple est que les microprocesseurs d’ordinateur sont relativement lents dans le calcul sur des nombres en virgule flottante (et la représentation suggérée ci-dessus sous forme de nombres rationnels pour e et e_(1,0) est nettement plus complexe et non nativement prise en charge par les processeurs ce qui augmente le nombre d’instructions pour travailler sur de tels nombres) ; de plus, les erreurs d’approximation du nombre flottant e_(1,0) s’accumulent à chaque addition de e_(1,0) dans e. Travailler avec uniquement des entiers permettrait un calcul à la fois plus exact et plus rapide.

La première astuce est de remarquer d’abord qu’on peut remplacer e par e-0,5, ce qui permet de ne tester que le signe de la valeur d’erreur au lieu de comparer deux rationnels, le test de proximité par rapport à la droite exacte revient alors à savoir lequel des deux pixels candidats se situe en dessous de la droite exacte parallèle dont les ordonnées sont augmentées de 0,5, et de remplacer l’arrondi de la formule (1) ci-dessus dans à l’entier le plus proche par un arrondi à l’entier égal ou inférieur avec cette nouvelle droite, ce qui ne change effectivement pas la formule (2) ci-dessus, mais e représentera l’erreur commise lors de l'approximation de cette seconde droite par les pixels tracés :

      procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est        déclarer entier x, y, dx, dy ;        déclarer rationnel e, e(1,0), e(0,1) ;  // valeur d’erreur et incréments        dy ← y2 - y1 ;        dx ← x2 - x1 ;        y ← y1 ;  // rangée initiale        e ← -0,5 ;  // valeur d’erreur initiale        e(1,0) ← dy / dx ;        e(0,1) ← -1.0 ;        pour x variant de x1 jusqu’à x2 par incrément de 1 faire          tracerPixel(x, y) ;          si (e ← e + e(1,0)) ≥ 0 alors  // erreur pour le pixel suivant de même rangée            y ← y + 1 ;  // choisir plutôt le pixel suivant dans la rangée supérieure            e ← e + e(0,1) ;  // ajuste l’erreur commise dans cette nouvelle rangée          fin si ;        fin pour ;      fin procédure ;      

Ensuite en multipliant tous les rationnels ci-dessus par dx, le calcul ne demande plus d’incréments rationnels (ce qui élimine l'accumulation d'erreurs d’approximation des flottants). Cependant la valeur initiale de e=-0,5×dx n’est pas encore entière, même si ses incréments sont entiers.

      procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est        déclarer entier x, y, dx, dy ;        déclarer rationnel e ; // valeur d’erreur        déclarer entier e(1,0), e(0,1) ;  // incréments        dy ← y2 - y1 ;        dx ← x2 - x1 ;        y ← y1 ;  // rangée initiale        e ← -0,5 × dx ;  // valeur d’erreur initiale        e(1,0) ←  dy ;        e(0,1) ← -dx ;        pour x variant de x1 jusqu’à x2 par incrément de 1 faire          tracerPixel(x, y) ;          si (e ← e + e(1,0)) ≥ 0 alors  // erreur pour le pixel suivant de même rangée            y ← y + 1 ;  // choisir plutôt le pixel suivant dans la rangée supérieure            e ← e + e(0,1) ;  // ajuste l’erreur commise dans cette nouvelle rangée          fin si ;        fin pour ;      fin procédure ;      

Toutefois en doublant e (et les valeurs de ses incréments), cela ne change rien au test de son signe : e représentera alors la distance par rapport à la droite exacte d’ordonnées augmentées de 0,5, cette distance étant multipliée par le facteur constant positif 2×dy (ce qui ne change pas le signe de la valeur d’erreur testée). La valeur de pente utilisée comme incrément de e étant aussi multipliée par le même facteur devient simplement 2×dy, sa valeur initiale devient -dx, le second décrément conditionnel devient 2×dx (que l’on peut aussi précalculer). L’algorithme devient alors :

      procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est        déclarer entier x, y, dx, dy ;        déclarer entier e ; // valeur d’erreur        déclarer entier e(1,0), e(0,1) ;  // incréments        dy ← y2 - y1 ;        dx ← x2 - x1 ;        y ← y1 ;  // rangée initiale        e ← -dx ;  // valeur d’erreur initiale        e(1,0) ←  dy × 2 ;        e(0,1) ← -dx × 2;        pour x variant de x1 jusqu’à x2 par incrément  de 1 faire          tracerPixel(x, y) ;          si (e ← e + e(1,0)) ≥ 0 alors  // erreur pour le pixel suivant de même rangée            y ← y + 1 ;  // choisir plutôt le pixel suivant dans la rangée supérieure            e ← e + e(0,1) ;  // ajuste l’erreur commise dans cette nouvelle rangée          fin si ;        fin pour ;      fin procédure ;      

Réduction des variables et simplifications

On pourra enfin changer le signe de e en testant le signe opposé, puis réduire le nombre de variables, en constatant que x1 et y1 ci-dessus ne sont plus utilisés dès que l’erreur initiale et les incréments sont calculés ; il suffit de changer aussi le signe des incréments et décréments :

      procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est        déclarer entier dx, dy ;        déclarer entier e ; // valeur d’erreur        e  ← x2 - x1 ;        // -e(0,1)        dx ← e × 2 ;          // -e(0,1)        dy ← (y2 - y1) × 2 ;  // e(1,0)        tant que x1 < x2 faire          tracerPixel(x1, y1) ;          x1 ← x1 + 1 ;  // colonne du pixel suivant          si (e ← e - dy) ≤ 0 alors  // erreur pour le pixel suivant de même rangée            y1 ← y1 + 1 ;  // choisir plutôt le pixel suivant dans la rangée supérieure            e ← e + dx ;  // ajuste l’erreur commise dans cette nouvelle rangée          fin si ;        fin faire ;        // Le pixel final (x2, y2) n’est pas tracé.      fin procédure ;      

Cet algorithme est optimal et suffisant pour tracer tout vecteur horizontal diagonal ou oblique dans le premier octant, de colonnes et rangées croissantes. Si le langage de programmation le permet, les deux variables locales déclarées x et y peuvent être remplacées par réutilisation des variables x₁ et y₁ des paramètres. Ce cas est traité ci-dessus.

Toutefois il faut remarquer dans l’algorithme ci-dessus que le test du signe de e peut aussi bien inclure l’égalité avec zéro ou ne pas l’inclure. Cela correspond au fait que les deux pixels suivants candidats sont équidistants de la droite exacte. Si on choisit un déplacement diagonal le deuxième point suivant sera toujours obtenu par un déplacement horizontal ; si on choisit un déplacement horizontal le deuxième point suivant sera toujours obtenu par un déplacement diagonal. Si on inversait la direction du vecteur, les pixels choisis seraient inversés donc différents, et on devra en tenir compte si on souhaite un recouvrement exact des pixels de deux vecteurs obliques de sens opposés, lors de la généralisation de l’algorithme à des vecteurs obliques de directions quelconques (ce cas ne peut pas se produire pour le tracé de vecteurs horizontaux, verticaux ou diagonaux).