Alvéole d'abeille - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
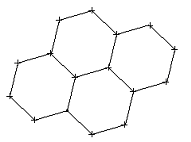
Les alvéoles d’abeilles, construits en cire par les abeilles ouvrières afin de stocker le miel et le pollen ou les œufs et les larves, sont des prismes juxtaposés d’axes horizontaux qui constituent le gâteau de cire. Ce gâteau de cire est ainsi formé de deux séries d’alvéoles hexagonaux se rejoignant en leur base.
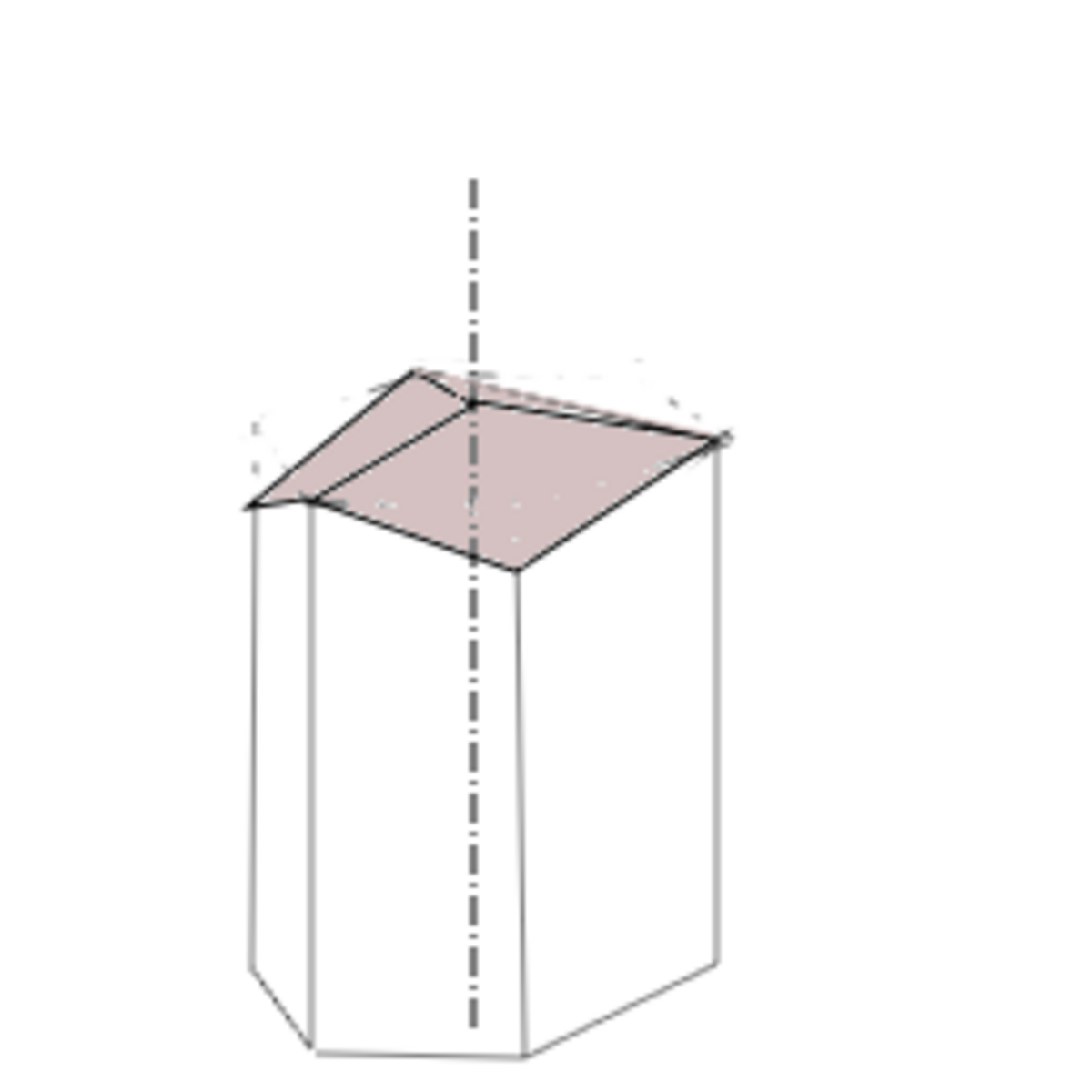
Mais ce qui est vraiment surprenant, c’est la forme plus que singulière de ces alvéoles. L’autre extrémité de ces cellules n’est pas un hexagone régulier, mais un emboîtement de trois losanges identiques, appelés rhombes. Les prismes ne se raccordent donc pas par leur surface hexagonale, mais justement par ces losanges, chaque cellule étant adossée, décalée, à trois autres au moyen de ces surfaces.
La construction de l’alvéole commence par le fond. L’épaisseur des parois est infime (moins de 300 micromètres, c’est diaphane-translucide), seul le bord supérieur est plus épais, pour éviter l’effritement.
Aperçu historique
La forme hexagonale des alvéoles fut repérée par Aristote dès le IVe siècle av. J.-C. (Histoire des animaux) puis traitée géométriquement huit siècles plus tard par Pappus, mathématicien grec ; mais ce n’est qu’au XVIIIe siècle que cette forme rhomboïdale fut remarquée. Ainsi, Maraldi, astronome à l’Observatoire de Paris, détermina expérimentalement en 1712 la valeur des angles de ces rhombes, égale à 109°28′ et 70°32′.
Intrigué par la complexité de ces formes, le physicien Réaumur soupçonne les abeilles de construire leur gâteau de cire dans un souci d’économie (voir l’article Apiculture). Afin de vérifier son hypothèse, il demanda au géomètre allemand König de déterminer quelle était la cellule hexagonale à fond composé de trois rhombes égaux qui pouvait être construite avec le moins de matière possible. Par calcul différentiel, König trouva en 1739 que les angles de ces losanges devaient être égaux à 109°26′ et 70°34′. La correspondance de ce résultat avec celui de Maraldi est déjà étonnante, mais elle fut améliorée en 1734 par le mathématicien écossais Maclaurin qui démontra que König avait commis une erreur dans ses calculs, et que les angles des losanges correspondant à l’utilisation d’un minimum de matière étaient justement ceux indiqués par Maraldi : 109°28′ et 70°32′ [les valeurs mathématiques optimales sont égales respectivement à Arc cos (-1/3) et Arc cos (1/3)]. c’est bien l’angle des faces de contact de 4 bulles de savon qui se rencontrent en un point. Les bulles de savon réalisent toujours, à cause de leur tension superficielle, la surface minimale à contrainte de contour donné.
C’est Réaumur qui propose l’idée originale et avant-gardiste de prendre comme unité de mesure le côté du pavage hexagonal et regrette beaucoup qu’il n’en fût pas fait de mesure dans les civilisations anciennes, car cela aurait donné une traçabilité des unités de mesure.
On retrouve sur ce problème : Lhuillier (Berlin, 1781), Lalanne (Ann.sc.nat. 1840), Brougham (CRAS, 1858) et Hennessy (proc. roy. soc. London, 1886), avec évidemment Buffon et Plateau. Buffon commet une erreur : son idée, souvent reprise hélas, est FAUSSE : qu’on comprime simultanément deux ensemble de cylindres de cire allongés ; ils prendront cette forme hexagonale. C’est possible, mais les abeilles ne procèdent pas de cette manière (HUBER, Paris, 1814, observation des abeilles) : elles commencent par construire le fond, puis les faces des cylindres hexagonaux ! Elles ont donc en elles une adaptation à la construction d’un tel gaufrage du fond. Cela procède certes du tassement simultané en recto-verso de la cire, et l’explication de Buffon n’est donc pas à négliger, mais cela ne correspond pas à une situation de toutes les alvéoles, ensemble, comme on le voit écrit parfois.