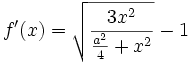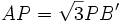Alvéole d'abeille - Définition

Pourquoi des rhombes ?

Le fond formé de trois rhombes permet un adossement simple des alvéoles. Il est même facile de prouver qu’il est plus économique qu’un fond plat hexagonal mais reste-t-il le moyen le plus économique ?

En 1964, Fejes Toth a démontré que si le fond était formé de deux petits hexagones ainsi que de deux losanges, à la place de trois rhombes, la quantité de cire serait, pour un même volume, inférieure de 0,35 % à ce qu’elle est avec les losanges.

Pourquoi un hexagone ?

Le premier souci des abeilles est de paver le plan pour pouvoir ensuite paver l’espace. On connaît trois polygones réguliers permettant de paver le plan : le triangle équilatéral, le carré et l’hexagone. Or, on peut démontrer que, parmi ces trois polygones réguliers, pour une même surface, l’hexagone est le polygone régulier offrant le plus petit périmètre.

Cependant, on pourrait se demander si l’hexagone est bien le pavage du plan le plus économique. En effet, on pourrait envisager de combiner des polygones de toutes sortes, qui ne sont pas forcément réguliers ni même dont les côtés forment une ligne droite. On ne savait pas grand-chose sur ce sujet jusqu’en 1943, date à laquelle le mathématicien hongrois Fejes Tóth démontra que la structure hexagonale régulière restait le polygone le plus économique pour paver le plan parmi tous les polygones à côtés droits.

Mais que se passe-t-il lorsque les côtés sont courbes ? Fejes Tóth pensait que la structure hexagonale régulière resterait la plus efficace, mais il ne parvint pas à le démontrer.

Ce n’est qu’en 1999 que Thomas C. Hales présente sa preuve en 19 pages (Honeycomb Conjecture).

Calcul des angles

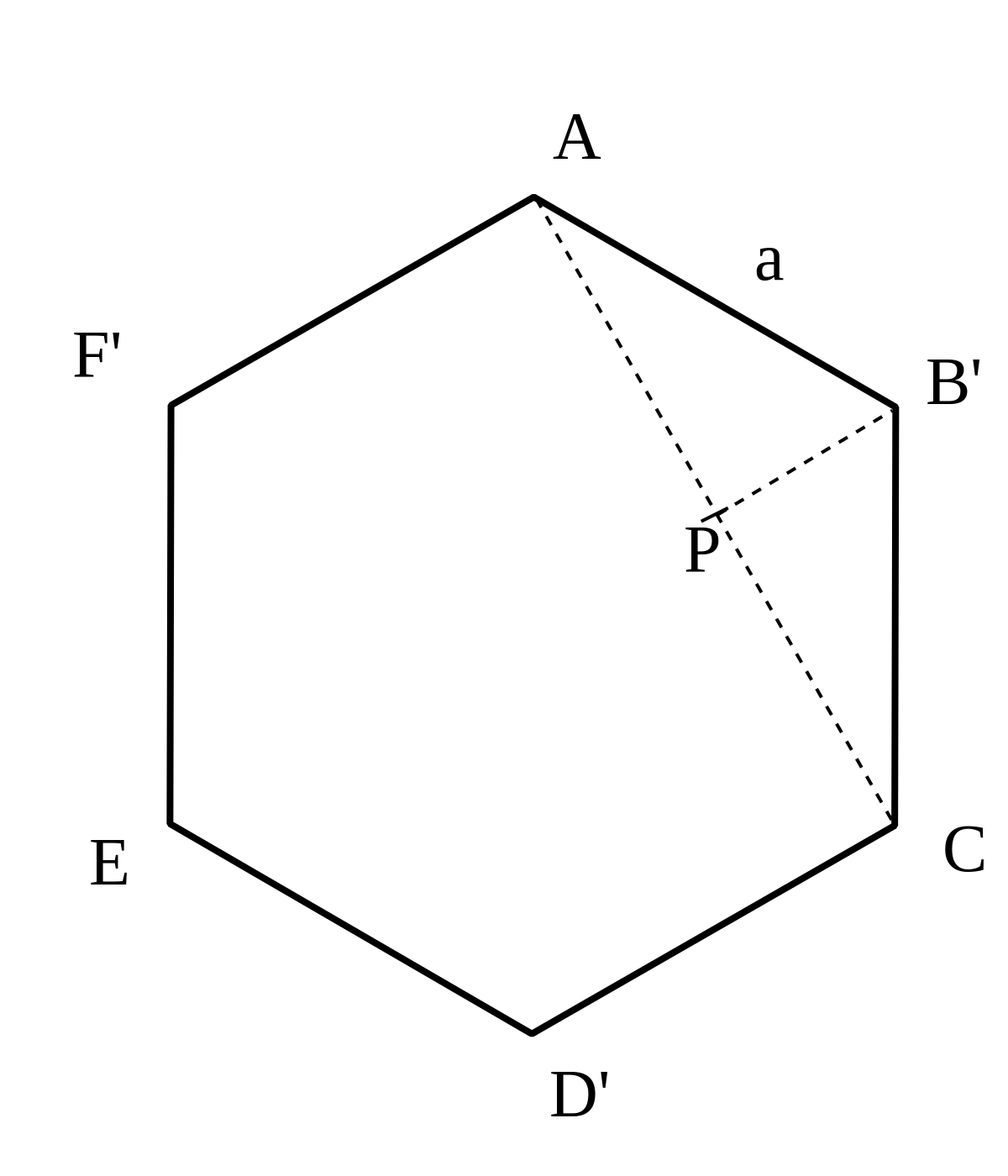
Pour déterminer les angles des rhombes minimisant la surface, on peut déjà remarquer que le remplacement d’un fond hexagonal AB′CD′EF′ par un fond formé de 3 rhombes de diagonales AC, CE, EF, ne modifie pas le volume de l’alvéole. En effet, le volume ôté est exactement égal au volume ajouté.

Il s’agit maintenant de comparer les surfaces.

Dans un fond rhomboïdal, la surface est celle de trois losanges SABC, SCDE, SEFA

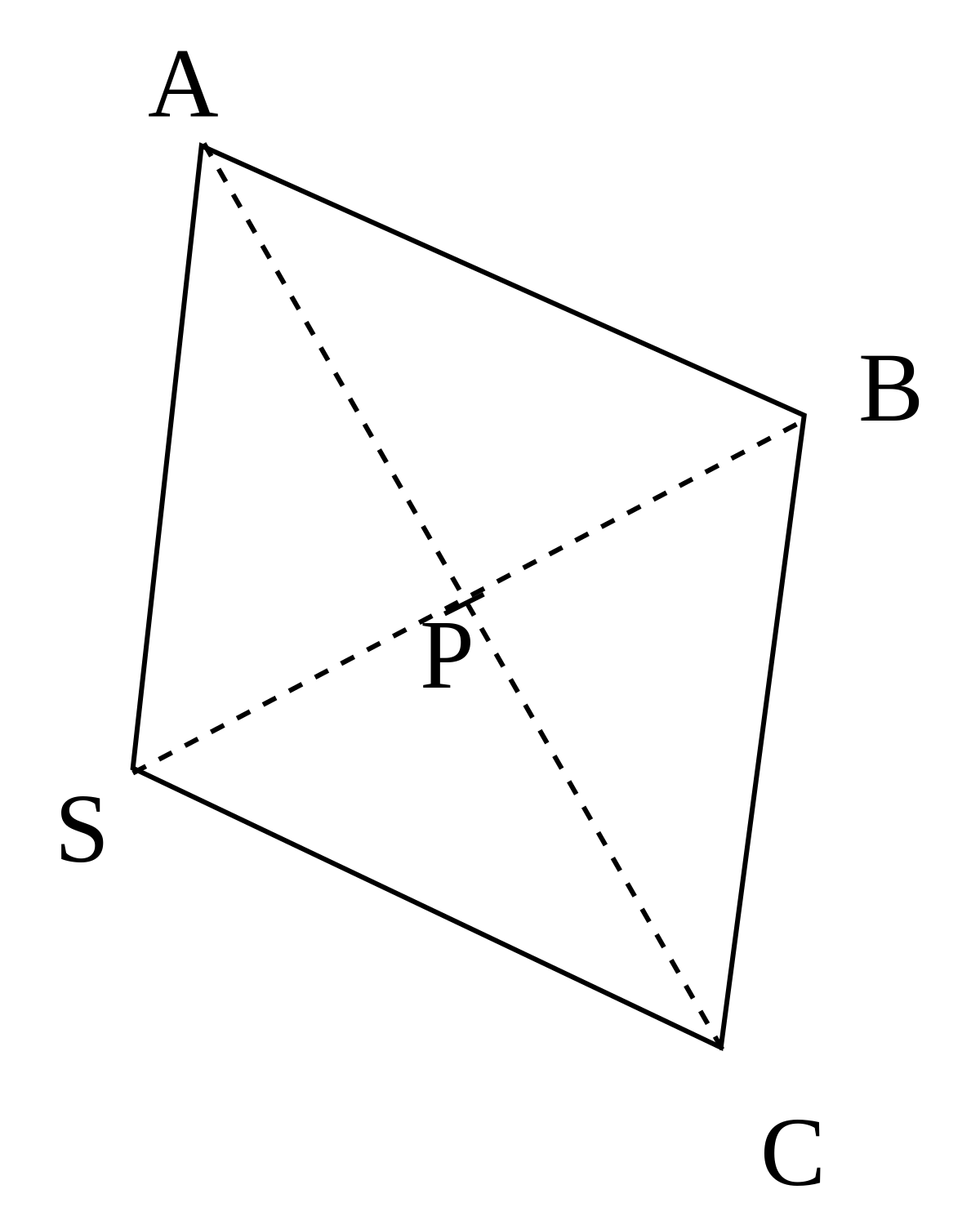
Cette surface remplace exactement la surface du fond hexagonal AB′CD′EF′ et de 6 triangles égaux au triangle AB′B.

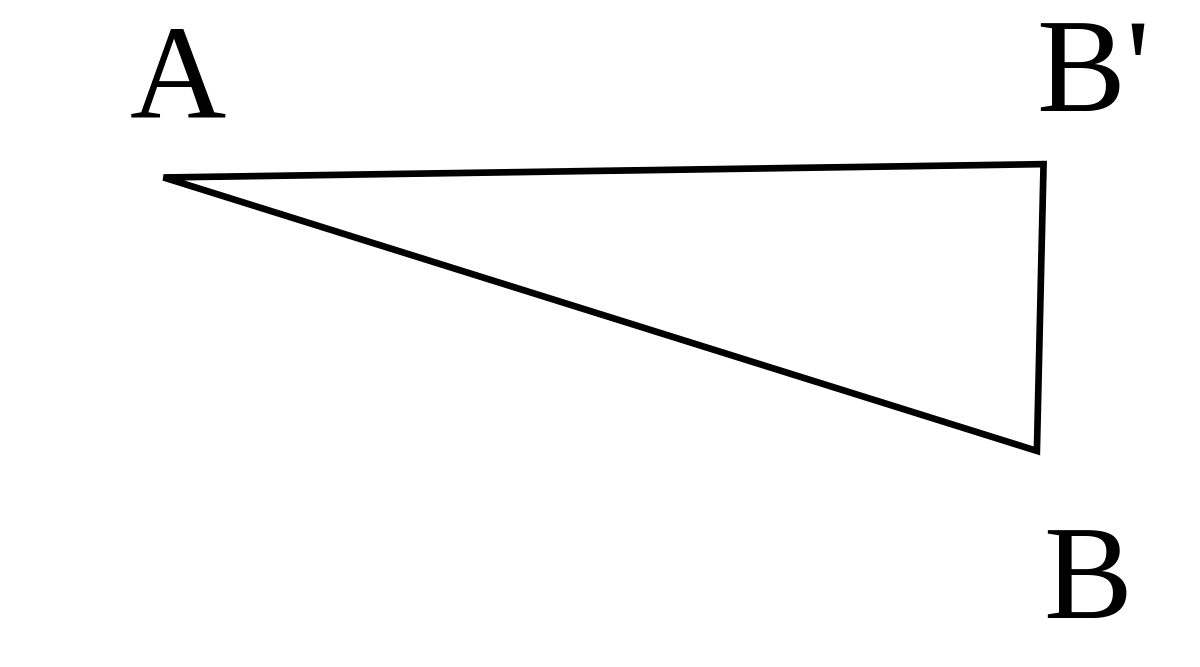
La position de B est optimale quand aire(SABC) - 2 × aire (AB′B) est minimale.

Or la diagonale du losange se calcule aisément . Si on appelle P le centre du losange, l’aire de SABC est alors .

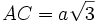
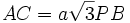
Quant au triangle AB′B, rectangle en B′, son aire vaut

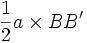
La quantité aire(SABC) - 2 × aire (AB′B) sera donc minimale si le chemin est minimal

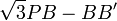
Deux méthodes sont alors possibles. L’une est accessible au niveau lycée, l’autre utilise le principe de Fermat.

Niveau lycée : on appelle x la longueur BB′, il s’agit alors de rendre minimale la quantité

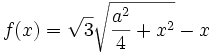
Le calcul de la dérivée mène à

C’est une fonction croissante sur (car est croissante) qui s’annule pour , c’est-à-dire lorsque .

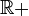
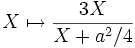
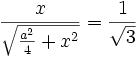
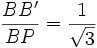
C’est donc pour ce rapport que la fonction atteint son minimum.

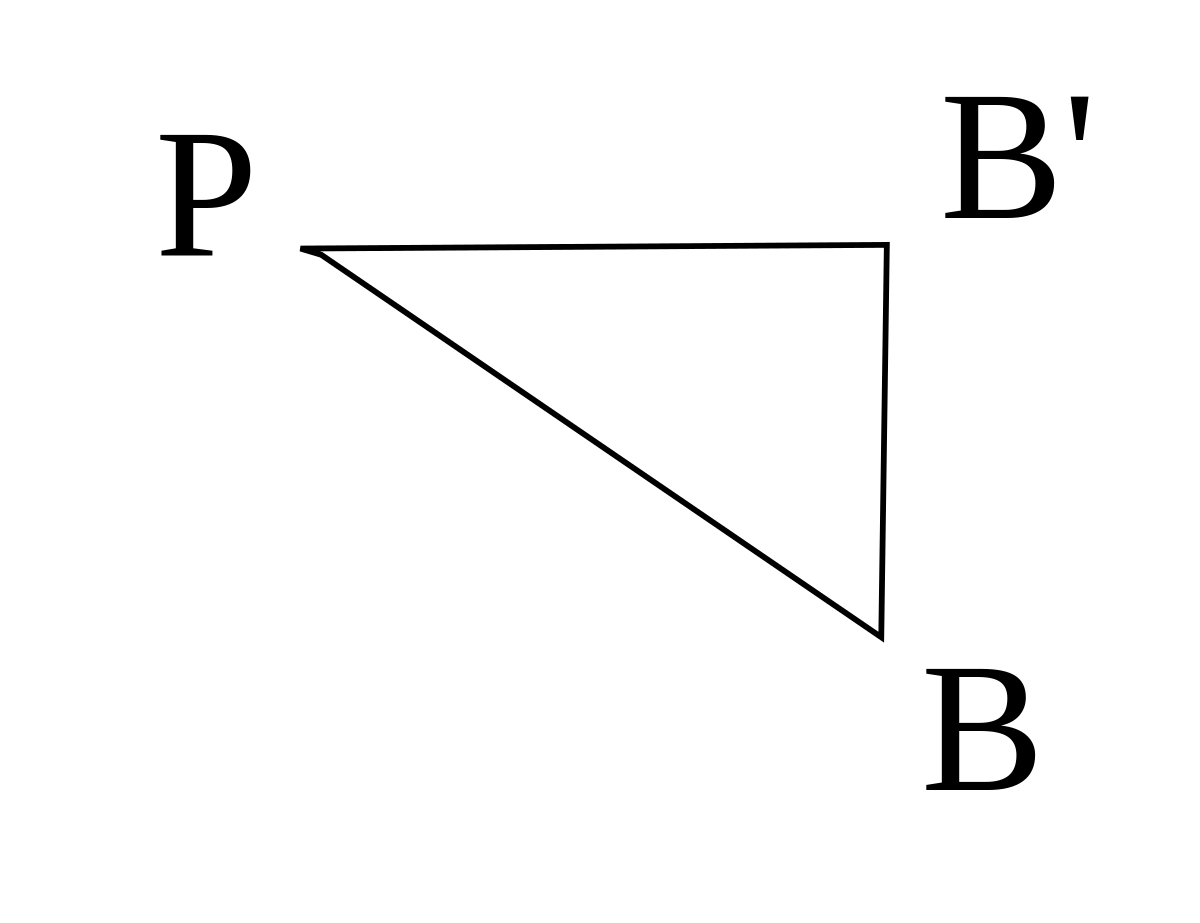
Principe de Fermat : il précise que le chemin est minimal lorsque est orthogonal à soit lorsque .

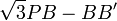
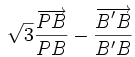
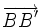
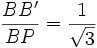
Il ne reste plus qu’à trouver les angles du losange. On appelle et

• Dans le triangle PB′B, on a

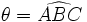
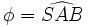
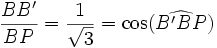
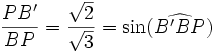
ce qui donne

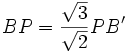
• Dans le triangle APB′

• Donc, dans le losange SABC, on a
  • , ce qui donne
  • , ce qui donne

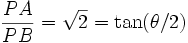
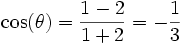
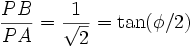
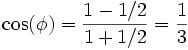
soit des angles de 109°28′ et de 70°32′, comme l’a trouvé Mac Laurin.

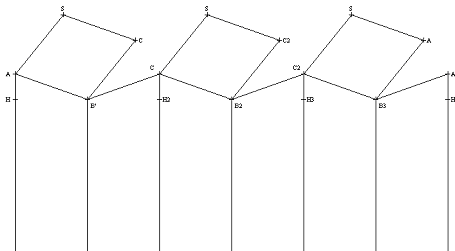
Développement d’un alvéole d’abeille