Beauté mathématique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Certains mathématiciens recherchent dans leur travail ou dans les mathématiques en général, un plaisir esthétique. Ils expriment ce plaisir en décrivant de « belles » parties des mathématiques.
Ils peuvent considérer les mathématiques comme un art ou comme une activité créative. Des comparaisons sont souvent faites avec la musique et la poésie.
Bertrand Russell a donné son sens de la beauté mathématique en ces termes : « Les mathématiques, considérées à leur juste mesure, possèdent non seulement la vérité, mais la beauté suprême, une beauté froide et austère, comme celle d'une sculpture, sans référence à une partie de notre fragile nature, sans les effets d'illusion magnifiques de la peinture ou de la musique, pourtant pur et sublime, capable d'une perfection sévère telle que seulement les plus grands arts peuvent la montrer. L'esprit vrai du plaisir, l'exaltation, l'impression d'être plus qu'un homme, qui est la pierre de touche de l'excellence la plus élevée, doit être trouvé dans les mathématiques aussi sûrement que la poésie. ».
Paul Erdős évoqua le caractère ineffable de la beauté des mathématiques en déclarant « pourquoi les nombres sont-ils beaux ? Cela revient à se demander pourquoi la neuvième symphonie de Beethoven est belle. Si vous ne voyez pas pourquoi, personne ne pourra vous l'expliquer. Je sais que les nombres sont beaux. S'ils ne sont pas beaux, rien ne l'est ».
La beauté dans les formules
Une formule est considérée comme « belle » si elle apporte un résultat essentiel et surprenant par sa simplicité par rapport à la complexité apparente (donc en particulier une égalité dont un des membres est très simple alors que l'autre membre est très compliqué).
Un exemple de belle formule est celle de Leonhard Euler eiπ + 1 = 0, dont Euler lui-même disait qu'elle montrait la présence de la main de Dieu.
Dans le roman Enigma, le mathématicien fictif Tom Jéricho qualifie de « cristalline » la beauté de la formule
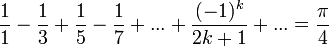
La beauté dans les théorèmes
Les mathématiciens voient la beauté dans les théorèmes mathématiques qui permettent de faire le lien entre deux domaines des mathématiques qui semblent à première vue totalement indépendants. Ces résultats sont souvent considérés comme « profonds ».
Certains exemples sont souvent cités dans la littérature scientifique. C'est le cas de l'identité d'Euler eiπ + 1 = 0 qui fut appelée « la formule la plus remarquable en mathématiques » par Richard Feynman. Les exemples modernes incluent le théorème de Taniyama-Shimura qui établit un lien important entre les courbes elliptiques et les formes modulaires (travail pour lequel ses auteurs Andrew Wiles et Robert Langlands reçurent le prix Wolf), et la « Conjecture Monstrous Moonshine » qui établit un lien entre le groupe Monstre et les fonctions modulaires par l'intermédiaire de la théorie des cordes pour laquelle Richard Borcherds se vit décerner la médaille Fields.
A contrario, un théorème trivial peut être une proposition qui se déduit de manière évidente et immédiate d'autres théorèmes connus, ou qui ne s'applique qu'à un ensemble spécifique d'objets particuliers tels que l'ensemble vide. Cependant, il arrive qu'un théorème soit suffisamment original pour être considéré comme profond, bien que sa démonstration soit assez évidente.


















































