Beauté mathématique - Définition
La liste des auteurs de cet article est disponible ici.
La beauté dans les méthodes
Les mathématiciens peuvent qualifier une méthode dans une démonstration d' « élégante » quand :
- Elle utilise peu de résultats préalables,
- Elle est exceptionnellement courte,
- Elle établit un résultat d'une façon surprenante (par exemple à partir de théorèmes qui ne sont apparemment pas en rapport avec celle-ci),
- Elle est basée sur des concepts originaux,
- Elle fait appel à une méthode qui peut être généralisée pour résoudre facilement une famille de problèmes semblables.
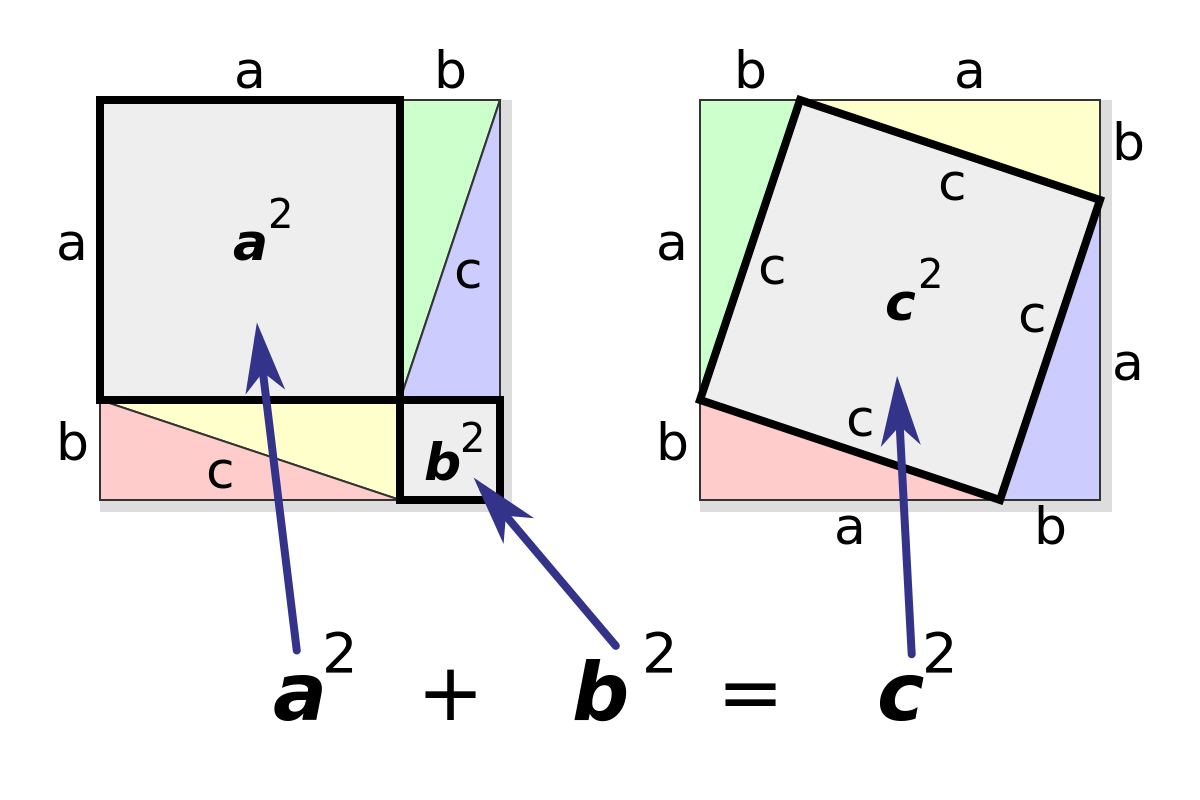
Dans la quête d'une démonstration élégante, les mathématiciens cherchent souvent différentes manières indépendantes d'établir un théorème ; la première démonstration trouvée peut ne pas être la meilleure. Le théorème pour lequel le plus grand nombre de démonstrations différentes a été trouvé est probablement le théorème de Pythagore puisque des centaines de preuves ont été publiées Modèle:Rf. Un autre théorème qui a été démontré de beaucoup de façons est le théorème de réciprocité quadratique de Karl Friedrich Gauss dont au moins huit démonstrations différentes ont été publiées.
Inversement, des méthodes logiquement correctes mais qui impliquent des calculs laborieux, des méthodes trop nuancées, des approches très conventionnelles, ou qui s'appuient sur un grand nombre d'axiomes particulièrement puissants ou sur des résultats préalables eux-mêmes habituellement considérés comme peu élégants, peuvent être qualifiées de laides ou de maladroites. Ceci est lié au principe du rasoir d'Occam.
Exemple très simple
Soit un train se déplaçant d'un point A à un point B à la vitesse de 10km/h.
La distance entre A et B est de 10km.
Soit une mouche qui part de B et qui fait des allers retours entre le point B et le train.
Cette mouche va à la vitesse constante de 60km/h (c'est une mouche très rapide.)
Elle fait constamment des allers retours entre le train et le point B et s'arrête dès que le train est arrivé.
On doit calculer quelle distance la mouche parcourt en tout.
Une première méthode non élégante consisterait à calculer les différents points où le train et la mouche se rencontrent, mettre cette distance sous la forme d'une suite, puis faire une somme infinie des termes de cette suite (lorsque le train va se rapprocher de l'arrivée, la mouche va rebondir très très vite, les points de rencontre vont tendre vers l'infini) et on obtient après de très longs calculs la réponse.
Une autre méthode dite élégante serait de constater que la mouche va s'arrêter en même temps que le train, c'est-à-dire au bout d'une heure, donc qu'elle aura parcouru exactement 60km.
Ce problème est classiquement posé dans l'unique but de tester l'aptitude d'un élève à choisir la méthode la plus simple.
La beauté et la philosophie
Certains mathématiciens s'accordent à dire que faire des mathématiques est plus proche de la découverte que de l'invention. Ils estiment que les théorèmes détaillés et précis des mathématiques peuvent être raisonnablement considérés comme vrais indépendamment de l'univers dans lequel nous vivons. Par exemple, certains prétendent que la théorie des nombres entiers naturels est fondamentalement valable, d'une manière qui n'exige aucun contexte spécifique. Des mathématiciens ont extrapolé ce point de vue en considérant la beauté mathématique comme une vérité, se rapprochant dans certains cas du mysticisme. Pythagore (et son école philosophique entière) croyaient en la réalité littérale des nombres. La découverte de l'existence de nombres irrationnels provoqua un grand désarroi au sein de l'école; ils considérèrent l'existence de ces nombres non exprimables comme rapport de deux entiers naturels, comme une poussière dans l'univers. Dans la perspective moderne, la vision mystique des nombres par Pythagore serait celle d'un numérologiste plutôt que celle d'un mathématicien.
Dans la philosophie de Platon il y a deux mondes, le monde physique dans lequel nous vivons et un monde abstrait différent qui contient la vérité invariable, y compris celle des mathématiques. Il pensait que le monde physique était un simple reflet du monde abstrait plus parfait.
On rapporte que Galilée prétendait que les « mathématiques sont la langue avec laquelle Dieu écrivit l'univers ».
Le mathématicien hongrois Paul Erdős, bien qu'athée, parla d'un livre imaginaire, dans lequel Dieu nota toutes les plus belles démonstrations mathématiques. Quand Erdős voulut exprimer sa satisfaction particulière d'une démonstration, il se serait exclamé « Celle-ci vient du livre ! ». Ce point de vue exprime l'idée que les mathématiques, étant la base intrinsèquement vraie sur laquelle sont établies les lois de notre univers, sont un candidat naturel pour être personnifiées en Dieu, selon différentes religions mystiques.
Le philosophe français du vingtième siècle Alain Badiou affirme que l'ontologie est des mathématiques. Badiou croit également en des liens profonds entre les mathématiques, la poésie et la philosophie.
Dans certains cas, les philosophes et les scientifiques qui ont beaucoup utilisé les mathématiques établirent des liens entre la beauté et la vérité physique de manières qui se sont avérées fausses. Par exemple, à une étape dans sa vie, Johannes Kepler crut que les proportions des orbites des planètes connues jusqu'alors dans le système solaire avaient été arrangées par Dieu pour les faire correspondre à un arrangement concentrique des cinq solides platoniciens, chaque orbite se trouvant sur la circonférence d'un polyèdre et l'insphere des autres. Comme il y a exactement cinq solides platoniciens, la théorie de Kepler ne pourrait seulement s'appliquer qu'à six orbites planétaires, et fut réfutée ultérieurement par la découverte d'Uranus. James Watson fit une erreur semblable quand il postula que chacune des quatre bases azotées de l'ADN est reliée à une base du même type se trouvant à l'opposé (thymine reliée à la thymine, etc.) en se basant sur la croyance que « ce qui est beau doit être vrai ».