Cadran bifilaire - Définition

Introduction

Cadran bifilaire

Inventé en 1922 par le mathématicien allemand Hugo Michnik, le cadran bifilaire est un modèle de cadran solaire qui présente la particularité d'indiquer l’heure par l'intersection de l’ombre de deux fils perpendiculaire au plan du cadran et non sécants, formant entre eux un certain angle (droit ou non). Il existe plusieurs possibilités de cadrans bifilaires

Cadran bifilaire horizontal

C'est le modèle qu'a découvert et étudié Hugo Michnik.
Un premier fil est orienté Nord-Sud et est situé à une distance constante du plan horizontal du cadran.

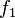
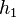
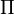
Un second fil est orienté Est-Ouest et est situé à une distance constante du plan (remarquer que est perpendiculaire à et est situé dans le plan du méridien).

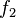
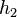
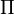
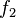
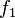
Appelons respectivement et la projection des fils et sur le plan , et leur intersection.
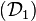
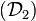
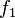
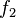
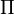
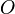
Définissons pour axe des abscisses Ox la droite orientée vers l'Est, et pour axe des ordonnées Oy la droite orientée vers le Nord.

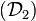
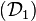
On peut montrer que si la position du soleil dans le ciel est connue et définie par ses coordonnées horaires et (respectivement angle horaire et déclinaison), alors les coordonnées et du point , intersection des ombres des 2 fils sur le plan du cadran, valent respectivement :

étant la latitude du lieu où est situé le cadran.

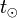
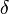
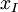
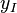
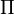
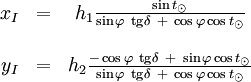
En éliminant la variable entre les deux relations précédentes, on obtient une équation reliant et et qui donne, en fonction de la latitude et de l'heure solaire (qui n'est autre que l'angle horaire du soleil), l'équation de la courbe horaire associée à une heure solaire donnée ; sous sa forme la plus simple à interpréter, cette équation peut s'écrire :

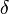
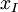
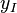
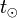
Cette relation montre que les courbes horaires sont des segments de droite et que les droites qui les portent passent toutes par le point de coordonnées :

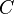
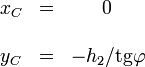
En outre, si l'on s'arrange pour que les deux hauteurs et soient telles que l'on ait :

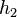
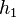
alors l'équation des lignes horaires s'écrit très simplement :

,

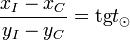
ce qui signifie qu'à tout moment, l'intersection des ombres des 2 fils sur le plan du cadran est telle que l'angle est égal à l'angle horaire du soleil et donc à l'heure solaire.

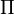
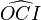
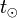
Ainsi, la particularité remarquable de ce type de cadran solaire bifilaire horizontal (qui respecte la condition ) est que les courbes horaires correspondant à une heure solaire donnée sont des demi-droites passant toutes par le point et que les 13 demi-droites correspondant aux heures successives 6h, 7h, 8h, 9h ... 15h, 16h, 17h, 18h sont régulièrement espacées d'un angle constant de 15°. Cette propriété s'appelle l'homogénéité des lignes horaires (suivant la terminologie proposée par Dominique Collin).

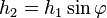
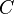
Un tel cadran bifilaire (horizontal et respectant la condition ) présente une autre propriété remarquable : il peut être déplacé le long d'un même parallèle (latitude constante) sans nécessiter la moindre modification dans le tracé des lignes horaires et des arcs diurnes.

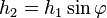
Cadran bifilaire incliné déclinant

Ce type de cadran n'a pas été étudié de façon aussi systématique que celui des cadrans verticaux mais il semble, d'après F. W. Sawyer (voir la référence ci-dessous) que l'on puisse conserver la propriété d'homogénéité des lignes horaires : il existe, comme dans le cas des cadrans bifilaire verticaux, deux relations à respecter portant sur l'orientation et la position des fils, mais celles-ci restent toutefois à établir...