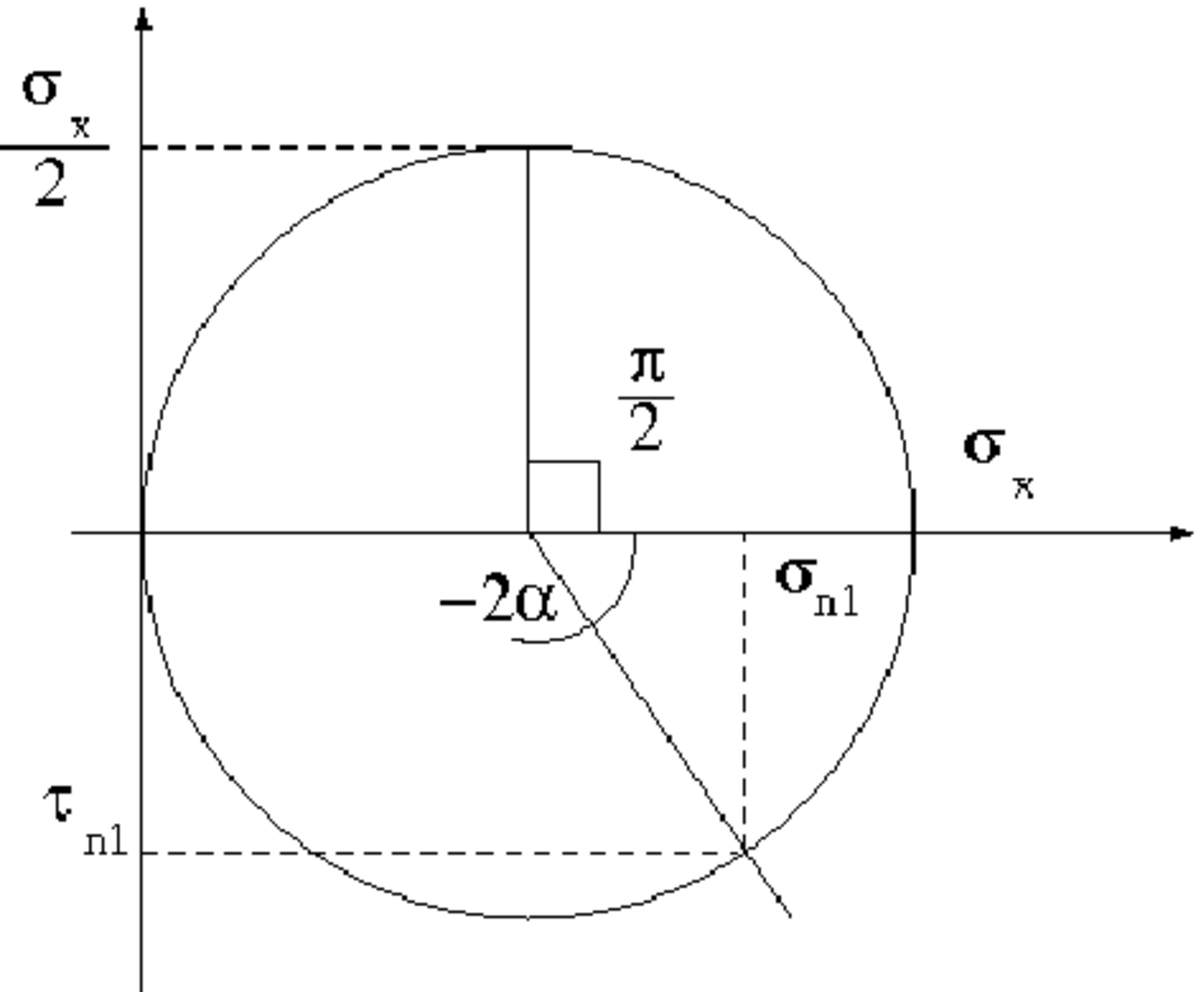
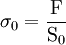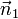Cercle de Mohr - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882.
Dans un graphique où l'axe horizontal représente l'amplitude de la contrainte normale et l'axe vertical représente l'amplitude de la contrainte de cisaillement, le cercle de Mohr est le lieu des états de contrainte en un point P lorsque le plan de coupe tourne autour du point P. Il s'agit d'un cercle centré sur l'axe horizontal dont les intersections avec l'axe horizontal correspondent aux deux contraintes principales au point P.
Ce cercle se construit à partir de la connaissance des efforts extérieurs auxquelles est soumise la pièce. Il permet de déterminer :
- les directions principales
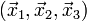
- la direction pour laquelle on a la cission τ maximale, qui est donc la direction de rupture probable (l'orientation du faciès de rupture), ainsi que la valeur de cette contrainte.
Problématique
La rupture d'un matériau ductile — c'est le cas de la plupart des métaux à température ambiante pour des vitesses de déformation modérées — se fait toujours en cisaillement : l'effort nécessaire pour « arracher » les atomes est beaucoup plus important que celui nécessaire pour faire glisser les atomes les uns sur les autres (voir Déformation plastique). Pour une sollicitation donnée d'une pièce, il faut donc savoir dans quelle section la cission τ (tau) est maximale.
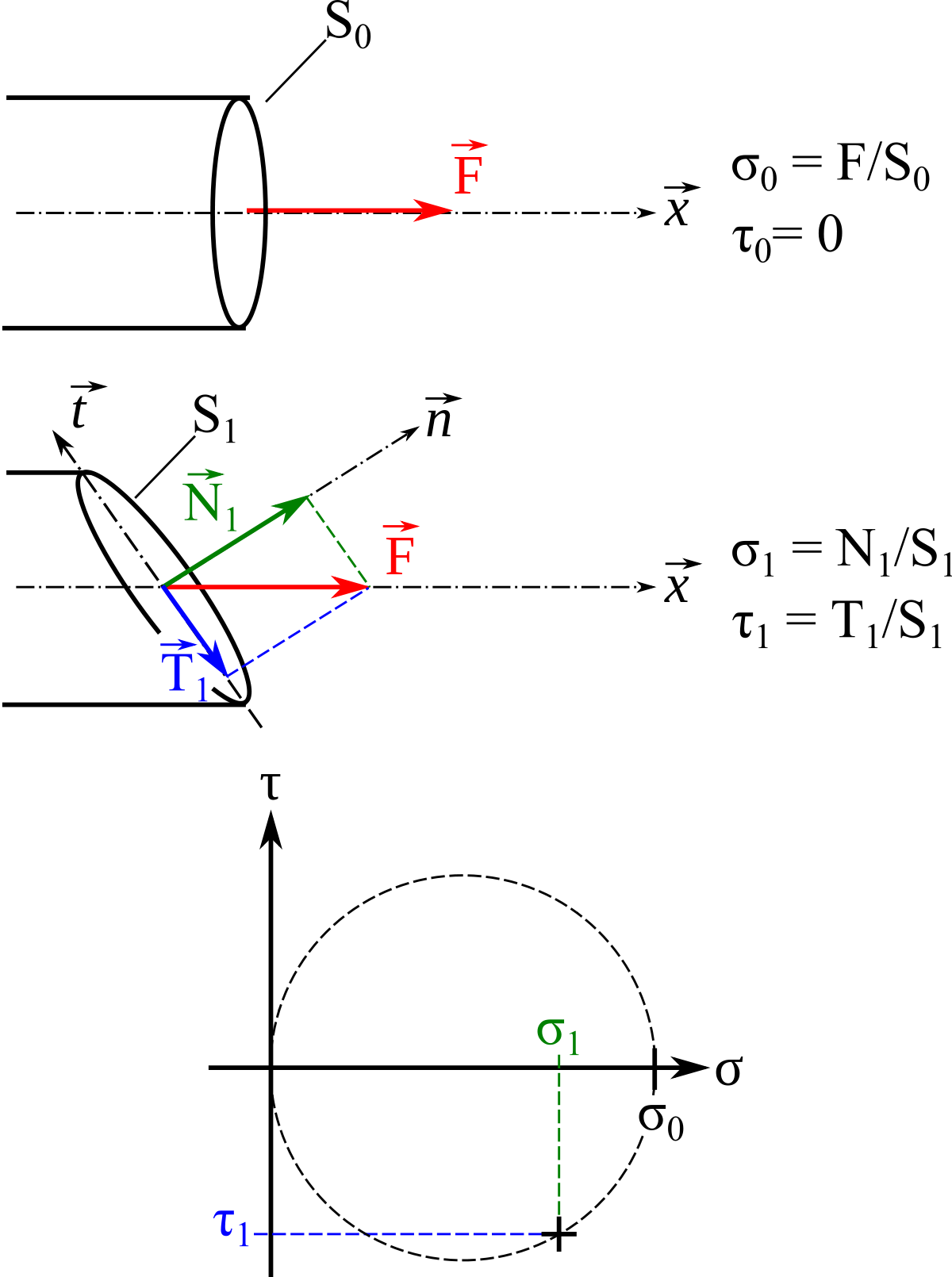
Prenons le cas de la traction simple, ou traction uniaxiale. On sait que lors de cet essai, le faciès de rupture va s'amorcer en faisant une direction de 45 ° par rapport à l'axe de l'éprouvette. Si l'on considère une section droite de l'éprouvette, celle-ci a une aire S0 ; la force F que l'on applique est normale à cette section, on a donc une contrainte normale σ0 qui vaut
et un cisaillement nul.
Considérons une section inclinée ; elle a une aire S1. si l'on projette la force
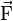
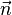
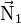
-
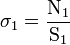
Si l'on projette
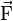
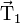
-
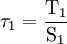
Plus la section est inclinée, plus T est grand, mais plus S est grand. La fraction τ = T/S présente un maximum pour une section située à 45 °, ce qui explique le faciès de rupture.
Si maintenant on trace τ = ƒ(σ), on voit que l'on obtient un cercle, le cercle de Mohr.
Cet exemple est repris ci-après de manière calculatoire.
Essais
Compression sur béton
Ci après la photo d'un essai de compression sur béton mettant en évidence le cône de rupture approximativement à 45°.
Essai de traction sur métal ductile
Aluminium
Ci après la photo d'un essai de traction sur une barre d'aluminium (diamètre 8 mm) .La rupture suivant une ligne à 45° est parfaitement illustrée.

Acier
Ci après la photo d'un essai de traction sur une éprouvette d'acier de section rectangulaire 10x3 mm. On remarquera les lignes à +/- 45° au voisinage de la zone rompue et les nombreuses facettes elles aussi à 45°.
Sollicitations axiales
Nous étudions ci-après le cas où l'on exerce une traction ou une compression selon les axes x, y et/ou z.
Sollicitation uniaxiale
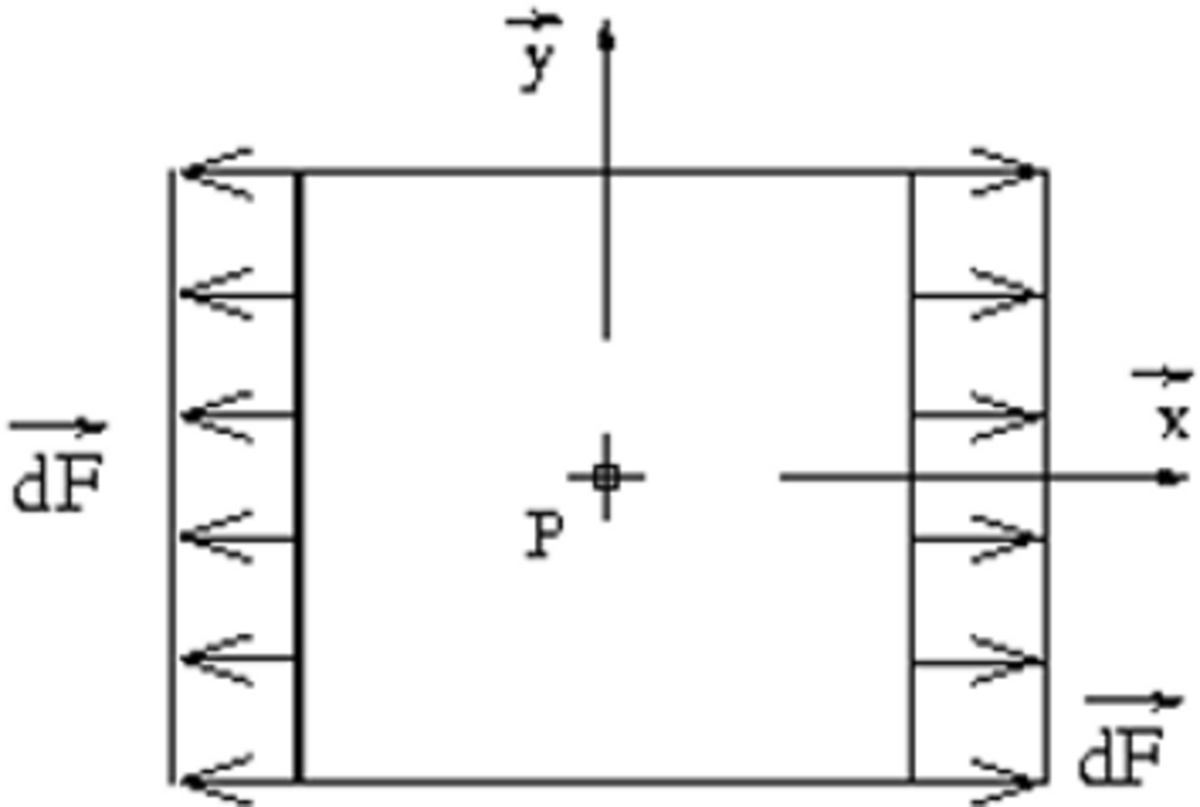
On réalise un essai de traction uniaxiale sur une éprouvette de laquelle on va extraire en un point P une plaquette infiniment petite soumise à un effort uniformément réparti
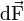
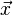
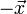
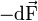
On notera
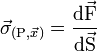
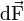
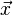
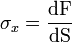
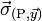
On remarquera que le cisaillement est nul sur les deux surfaces considérées, les directions
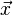
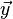
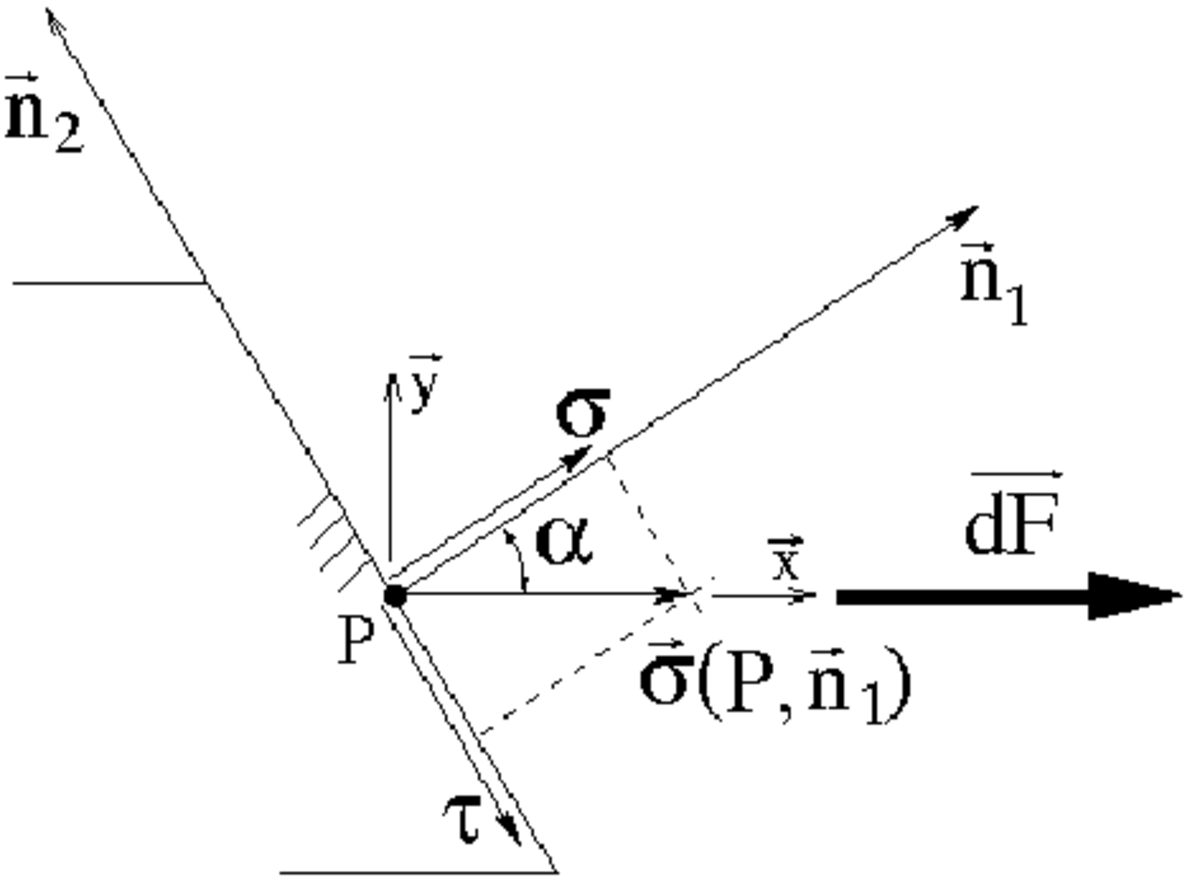
On détermine maintenant l'état de contrainte sur une face qui aurait tourné de α comme représenté sur le schéma ci-contre.
On a les contraintes suivantes :
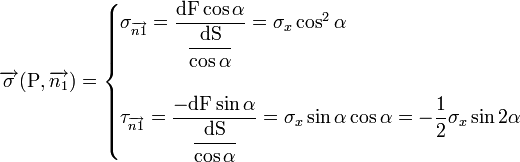
C'est l'équation d'un cercle de centre
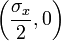
On observe que le cisaillement est maximal :
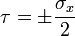
Sollicitation biaxiale
Sollicitation triaxiale
Dans ce cas la représentation ne présente pas un grand intérêt car les lieux du vecteur contrainte ne sont plus sur un cercle mais sur la surface délimitée par l'intersection des cercles.