Compacité séquentielle - Définition

Diverses propriétés

Opérations ensemblistes, théorème de Tychonoff

Propriété : Soit E un espace topologique, K₁ et K₂ deux parties compactes de E. Alors et sont compactes.

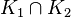
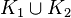
Propriété : Soit K₁ et K₂ deux espaces compacts ; le produit , muni de la topologie produit, est encore compact.

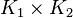
Théorème (de Tychonoff) : Un produit quelconque de compacts est compact, i.e. : si est une famille quelconque d'espaces compacts, alors le produit est encore un espace compact. (Ce théorème nécessite l'axiome du choix pour sa démonstration.)

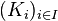
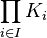
Compacité et continuité, théorème de Heine

Propriété : Soit E, F des espaces topologiques, F étant séparé, K une partie compacte E, et f une application continue de E vers F. Alors f(K) est compact.

Moralité : l'image continue d'un compact (dans un séparé) est compacte.

Corollaire : Soit K un espace compact, et f une application continue de K vers . Alors f est bornée et atteint ses bornes.

Propriété : Soit K un espace compact, F un espace séparé, et f une bijection continue de K vers F. Alors f est un homéomorphisme.

Théorème (de Heine) : Soit K un espace métrique compact, F un espace métrique, f une application continue de K vers F. Alors f est uniformément continue.