Compacité séquentielle - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Première approche : fermés bornés en dimension finie - Recouvrements ouverts - Les compacts dans le cadre des espaces métriques - Espaces métriques compacts - Diverses propriétés

Recouvrements ouverts

Un espace topologique non vide $K$ est dit compact s'il est séparé, et si de tout recouvrement ouvert de $K$ on peut extraire un sous-recouvrement fini.

Parties compactes

Une partie $K$ d'un espace topologique $X$ est dite compacte si le sous-espace topologique $K$ , muni de la topologie induite, est compact.

Une partie $K$ d'un espace topologique $X$ est dite relativement compacte si son adhérence $\bar{K}$ est une partie compacte de $X$ .

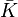
Cas des espaces métriques

Un espace métrique $K$ est dit précompact s’il en existe des recouvrements par des boules ouvertes arbitrairement petites, soit :

$\forall \epsilon>0\ \exists (x_i)_{1\leq i \leq n}\ /\ K \subset \bigcup_{i=1}^n B(x_i,\epsilon)$

Propriété : Un espace métrique est compact si et seulement s’il est précompact et complet

ATTENTION : Il faut se garder, dans le cas général, de dire que si un espace est compact alors il est complet et précompact ; en effet ces deux dernières notions sont métriques et n'ont donc aucun sens dans le cadre de la topologie générale. La compacité par contre est une notion « purement topologique ».

Propriété : Un espace métrique compact (ou une partie compacte d'un espace métrique) est borné(e). Il suffit en effet de considérer comme recouvrement les boules ouvertes de même centre et de rayon n ou n est entier. C'est un recouvrement, un recouvrement fini est inclus dans une boule et la propriété est démontrée.

Les compacts dans le cadre des espaces métriques

De très nombreux problèmes de topologie et d'analyse fonctionnelle se posent dans le cadre des espaces vectoriels normés de dimension quelconque, ou plus généralement des espaces métriques. L'outil principal est alors la notion de suite convergente.

Définition séquentielle

Dans ce cadre, il est possible d'adopter une définition séquentielle des compacts, en les définissant comme les parties vérifiant la propriété de Bolzano-Weierstrass. Ainsi K sera un compact si et seulement si de toute suite d'éléments de K on peut extraire une sous-suite qui converge dans K.

Dans le cas particulier d'un espace vectoriel normé de dimension finie, on a vu que les compacts sont les parties fermées bornées. En général, les compacts sont encore des parties fermées et bornées, mais la réciproque est fausse.

En reprenant la démonstration faite précédemment, l'image d'un compact par une application continue est un compact.

Exemples d'espaces compacts

Dans un espace vectoriel normé, une boule fermée est compacte si et seulement si l'espace est de dimension finie : c'est le théorème de Riesz.

Espaces métriques compacts

Dans le cas où l'on dispose d'une distance sur l'espace, on peut tirer de la compacité de nombreuses informations. On a déjà vu les interactions avec la complétude et la précompacité. On peut également caractériser la compacité à l'aide du théorème fondamental suivant.

Le théorème de Bolzano-Weierstrass

On dira qu'un espace métrique $E$ possède la propriété P si pour toute suite de points de E, on peut extraire une sous-suite convergeant vers un point de $E$ .

Cette propriété se dit également : toute suite d'éléments de $E$ a une valeur d'adhérence dans $E$ .

NB: Le fait que la limite soit dans l'espace est fondamental ; par exemple toute suite de points de $[0,1[$ admet une sous-suite convergente dans $\R$ mais la limite peut être $1$ .