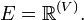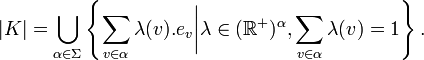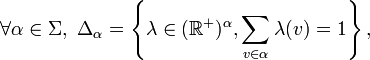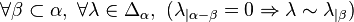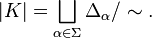Complexe simplicial - Définition

Approche combinatoire

Puisque chaque simplexe est entièrement déterminé par l'ensemble de ses sommets, un complexe simplicial géométrique peut être identifié à l'aide d'un objet combinatoire associé : le complexe simplicial abstrait.

Définition

Un complexe simplicial abstrait est la donnée d'un ensemble V (dont les éléments sont appelés sommets) et d'un ensemble Σ de parties finies non vides (les faces) de V qui soit stable par sous-parties non vides. Autrement dit, toute partie non vide d'une face est aussi une face. Il est en général requis que tout sommet appartienne à un nombre fini non nul de faces.

Les faces de cardinal 2 sont aussi appelées arêtes en référence au vocabulaire de la théorie des graphes. Par analogie, pour tout entier n, une face de dimension n (dite aussi n-face) est une face de cardinal n+1.

Si la dimension des faces est bornée, la dimension d'un complexe simplicial est la dimension maximale des faces. Dans le cas contraire, cette dimension est infinie.

Un complexe de dimension 0 est donc simplement un ensemble sans structure additionnelle. Un complexe de dimension 1 est un graphe.

La relation de sous-complexe est définie par l'inclusion de l'ensemble des sommets et l'inclusion de l'ensemble des faces.

Cas particuliers et opérations

• Sur tout ensemble X sans structure additionnelle, il existe un unique complexe simplicial (combinatoire) de dimension 0. Il s'agit de l'ensemble des singletons de X. Sa réalisation topologique est X muni de la topologie discrète.
• Sur tout ensemble fini non vide V de cardinal n+1, il existe un unique complexe simplicial de dimension n, défini par l'ensemble des sous-parties finies de V. Sa réalisation topologique est un simplexe de dimension n.
• Plus généralement, pour tout ensemble V et pour tout entier naturel n, l'ensemble des parties de V de cardinal au plus n+1 forment un complexe simplicial de dimension n.
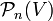
• Pour tout entier naturel n, le n-squelette d'un complexe simplicial (V;Σ) est défini par l'ensemble des faces de dimension inférieure ou égale à n + 1. Autrement dit, .
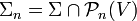
• La restriction d'un complexe simplicial à un sous-ensemble de sommets est défini par l'ensemble des faces incluses dans ce sous-ensemble. Autrement dit, .
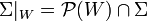
• La réunion de deux complexes simpliciaux ayant des ensembles de sommets disjoints est définie par les réunions de faces (α∪β) où α et β sont des faces respectives des complexes initiaux.
• La subdivision barycentrique d'un complexe simplicial K = (V,Σ) a pour sommets les faces de K et pour faces les ensembles finis non vides de faces de K totalement ordonnés par l'inclusion. La subdivision barycentrique d'un triangle plein est ainsi composée de sept sommets, de douze arêtes et de six faces triangulaires.

Réalisation géométrique

Étant donné un complexe simplicial K = (V,Σ), sa réalisation géométrique (notée |K|) est un espace topologique construit par recollement de simplexes, qui étendent en toute dimension la suite : segment, triangle, tétraèdre…

Constructions

Une première méthode de construction la produit comme partie d'un espace vectoriel réel dont une base (e_v) décrit l'ensemble des sommets de K, par exemple l'ensemble des applications presque nulles de l'ensemble des sommets dans l'ensemble des réels :

Si l'ensemble des sommets est fini, cet espace vectoriel est muni d'une unique topologie séparée. Cependant, si l'ensemble des sommets est infini, la topologie à considérer sur cet espace vectoriel n'est pas la topologie produit mais la topologie cohérente ou topologie faible<. L'adjectif « faible » (en anglais : weak) se retrouve dans le « W » de CW-complexe.

La réalisation géométrique est alors définie comme la réunion des enveloppes convexes des faces combinatoires, c'est-à-dire :

Une autre méthode consiste à définir une union disjointe de tous les simplexes à l'aide de coordonnées barycentriques puis à la quotienter de façon à réaliser le recollement, autrement dit :

L'intérêt de cette seconde méthode est qu'elle s'étend à la réalisation des ensembles simpliciaux.

Propriétés

Cette topologie confère à | K | une structure de CW-complexe. En particulier, un complexe simplicial est un espace topologique séparé et même normal. Une partie de cet espace est fermée si et seulement si son intersection avec chaque cellule (ici les cellules sont les n-faces) est fermée.

• Un complexe simplicial de dimension 0 est un espace topologique discret.
• Un complexe simplicial de dimension 1 est un graphe.
• Un complexe simplicial de dimension 2 est un espace triangulé.
• Plus généralement, en toute dimension, on appelle triangulation d'un espace topologique un homéomorphisme entre cet espace et un complexe simplicial. Bien sur, tout espace topologique n'est pas triangulable.

Cette construction historique est assez restrictive :

• Dans cette construction, les sommets d'une face sont distincts ; de plus, deux faces ne peuvent pas avoir exactement les mêmes sommets. Il faut par exemple au minimum 14 triangles, 21 arêtes et 7 sommets pour trianguler un tore.^{[réf. souhaitée]} D'où l'idée de lever ces restrictions. Cela mène à la structure de Δ-complexe. Avec cette nouvelle structure, deux triangles suffisent pour représenter un tore, une sphère ou un plan projectif. le calcul des groupes d'homologie s'en trouve grandement simplifié.